Valutazione delle distanze

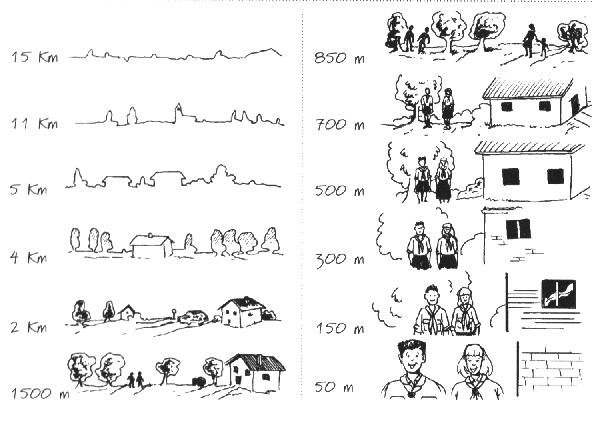
Con un po’ di esperienza e con molto esercizio, potrai imparare a valutare le distanze a colpo d’occhio. Ricorda, però, che ci sono condizioni che fanno sembrare gli oggetti più vicini, mentre ve ne sono altre che li fanno sembrare più lontane.

Gli oggetti ti sembrano più vicini quando:

• L’atmosfera è molto limpida (ad esempio dopo un temporale);
• La luce è viva e vi batte sopra;
• Fra te ed essi c’è una superficie di acqua, di neve, o di sabbia;
• Il terreno è piatto;
• Da mezza costa di una collina guardi verso l’alto o verso il basso.

Gli oggetti ti sembrano più lontani quando:

• Il terreno è accidentato;
• Sono in ombra;
• Fa molto caldo e c’è umidità nell’aria; c’è poca luce (sei al crepuscolo o c’è foschia);
• Guardi attraverso una valle;
• Lo sfondo è del loro medesimo colore;
• Sono in fondo a un viale o a una lunga strada dritta;

Misurazione delle distanze

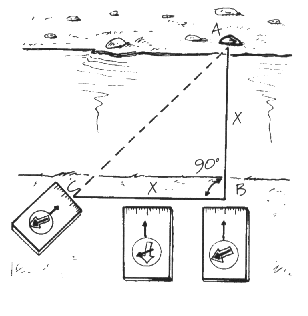
Il metodo della bussola

Stando su un lato del fiume (punto B) individua un punto evidente dall’altro lato (roccia A).
Rileva l’azimut della direzione BA (ad es. 120°).
Aggiungi 45° all’azimut della direzione BA (120° + 45° = 165°).
Cammina lungo il fiume perpendicolarmente ala direzione BA tenendo la bussola orientata verso l’azimut di 165°. Quando con questo azimut riuscirai a vedere nel mirino la roccia A, fermati. La distanza CB è uguale alla larghezza del fiume.

Il metodo dei millesimi

Per misurare le distanze con una buona precisione, puoi utilizzare il sistema dei "millesimi".
Il millesimo, o grado millesimale, è l’angolo sotto il quale si vede 1 metro quando si è alla distanza di 1 km.
Con questo sistema l’angolo gira è diviso in 6400 millesimi, o gradi millesimali (si indicano con °°).

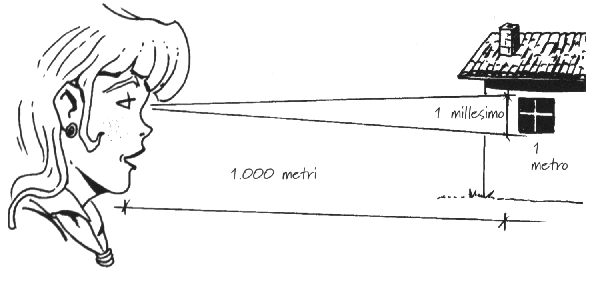
Se riesci a misurare sotto quale angolo millesimale vedi un certo oggetto del quale conosci le dimensioni (ad esempio una casa), puoi calcolare la distanza che c’è tra te e la casa, applicando la formula seguente:

Ad esempio, se vedi una casa alta 10 metri sotto un angolo di 5 millesimi, questo significa che la casa si trova a 2 km di distanza. Infatti:

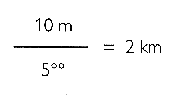
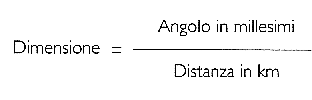
Viceversa, se conosci la distanza, puoi calcolare la dimensione dell’oggetto con il calcolo seguente:

Il metodo del cappello di Napoleone

Stando sulla riva del fiume individua un oggetto ben visibile sull’altra sponda. Inclina il cappellone in modo da traguardare il punto prescelto con la tesa dello stesso cappellone.
Senza alzare né abbassare la testa, girati su te stesso fino a trovare sulla tua riva un punto che sia allineato con la tesa del cappellone.
La distanza fra te e questo punto è uguale alla larghezza del fiume.

Il metodo del pollice

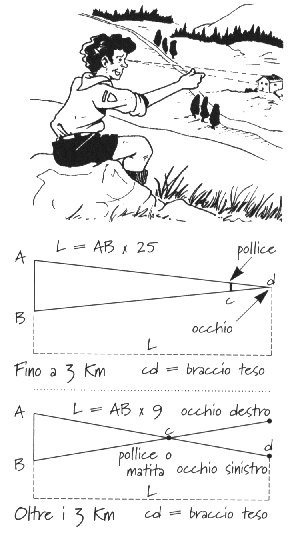
Il tuo pollice può esserti molto utile per valutare con buona approssimazione le distanze. Puoi adoperarlo in due modi, uno è valido per distanze inferiori a 3 km, l’altro per distanze maggiori.

Fino a 3 km:

Stendi il braccio con il pollice alzato davanti agli occhi e copri con esso un oggetto che si trovi alla distanza cercata e che sia facilmente valutabile, ad esempio la larghezza di una finestra, la facciata di una casa, ecc. La distanza fra te e quell’oggetto si ottiene moltiplicando per 25 la larghezza dello spazio coperto dal pollice.

Oltre 3 km:

Stendi il braccio con il pollice (oppure con una matita) alzato davanti agli occhi. Traguarda prima con l’occhio destro, poi con il sinistro sempre tenendo immobile la mano. Valuta la distanza tra i due punti traguardati e moltiplica per 9, otterrai la distanza che c’è fra te e i punti traguardati. Esercitati in varie circostanze e su terreni differenti perché se la teoria è semplice non sempre lo è la pratica.

N.B.: Nelle figure non sono rispettate le proporzioni.

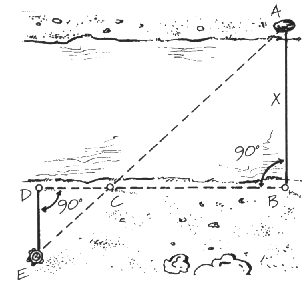
Il metodo delle perpendicolari

Individua un oggetto (A) ben visibile sull’altro lato del fiume. In corrispondenza ad esso, pianta un bastone (B) sulla tua riva.
Cammina lungo la riva, perpendicolarmente alla direzione AB, per una certa distanza, ad es. 50 metri. Pianta qui un altro bastone (C).
Continua a camminare per una distanza uguale alla precedente (altri 50 metri). Pianta qui un terzo bastone (D).
Ora cammina perpendicolarmente alla direzione BD. Quando vedrai allineati il bastone C con il punto A fermati. La distanza DE è uguale alla larghezza del fiume. Se sulla riva del fiume vi è poco spazio (vedi disegno), puoi percorrere una distanza CD pari alla metà di BC. In tal caso la distanza DE sarà pari alla metà della larghezza del fiume.

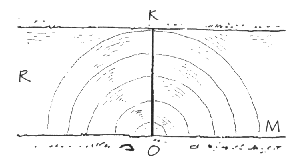
Il metodo del sasso

Per valutare la larghezza di un corso d’acqua, mettiti sulla sua riva nel punto O, e lascia cadere un sasso verticalmente nell’acqua.
Se l’acqua è calma, dal punto O dov’è caduto il sasso, partono dei cerchi concentrici che si allontaneranno sempre più. Segui con gli occhi uno di questi cerchi e, nel momento preciso in cui esso tocca la riva opposta nel punto K, cerca il punto M in corrispondenza della riva lungo la quale sei tu. Misura la distanza OM, essa sarà uguale alla distanza OK.

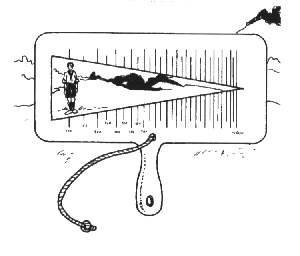
La stadia

La stadia è uno strumento molto semplice che serve per misurare le distanze.
Essa si compone di un pezzo di cartoncino o di legno di forma rettangolare, nel quale è intagliato un triangolo isoscele, come in figura.
Uno spago, da tenere fra i denti, ti consente di tenerla sempre alla stessa distanza dai tuoi occhi. Per usare questo strumento devi graduarlo. Per fare ciò, vai con un’altra persona di altezza media (circa m 1,70) in aperta campagna e mandala successivamente a 100 metri, a 150 metri, a 200 metri, ecc.
Ogni volta osservala fra quali punti del triangolo vedi compresa tutta la persona e segna su quei punti la distanza (in metri) a cui si trova la persona.
Una volta che hai graduato la stadia, quando vuoi misurare una distanza, guarda una persona attraverso il triangolo, facendo muovere lo strumento da una parte o dall’altra finché vedi la persona compresa all’interno del triangolo: la distanza riportata sul triangolo è la distanza cercata. La stadia serve solo per la persona che l’ha graduata, quindi ognuno deve averne una per sé.

La stadia millesimale

Per misurare gli angoli millesimali in maniera precisa, puoi fabbricarti unna stadia millesimale.
Prendi un doppio decimetro, lega ad esso una cordicella e fai un nodo all’altro capo della cordicella in maniera che la distanza fra il nodo e il doppio decimetro sia di 50 cm.

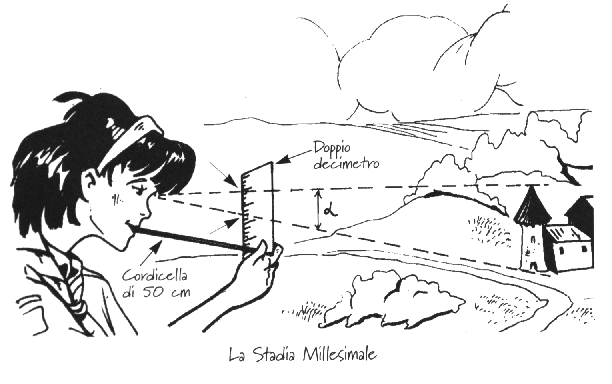
Tendi la cordicella, tenendo il nodo fra i denti, in questa maniera manterrai il doppio decimetro sempre alla distanza di 50 cm dai tuoi occhi.
Se tieni tesa la cordicella, le graduazioni del doppio decimetro coprono gli angoli seguenti:

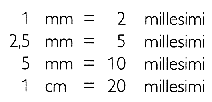
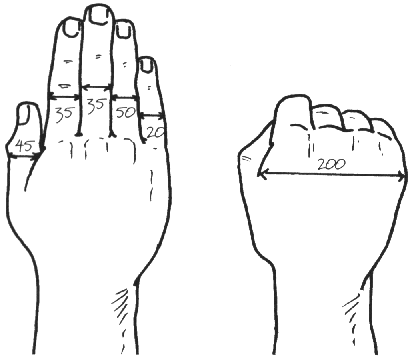
se non hai il doppio decimetro, puoi utilizzare la tua mano, ponendola davanti agli occhi con il braccio teso.
Nella figura puoi vedere quanti gradi millesimali copre approssimativamente ciascun dito.