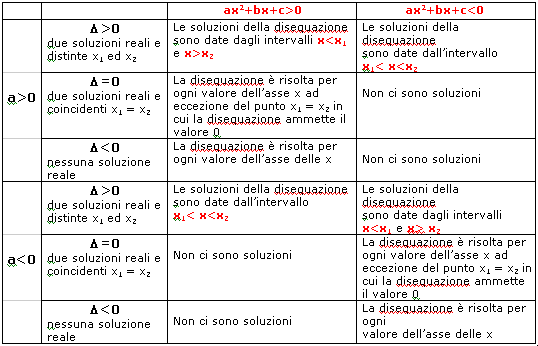
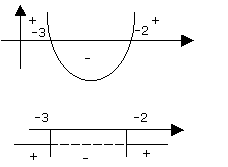
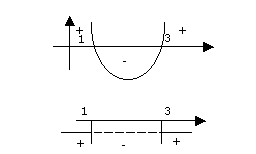
la curva rappresentata da una equazione di secondo grado č una parabola di equazione y=ax2+bx+c con la concavitą rivolta verso l'alto quando a>0, con la concavitą rivolta verso il basso quando a<0;
caso a>0
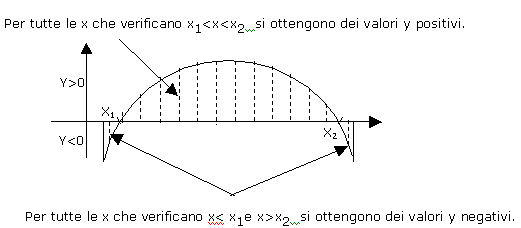
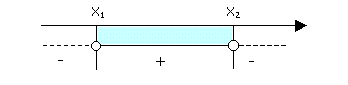
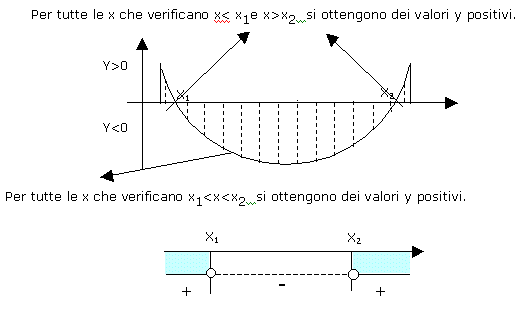
1) se D=b2-4ac >0 D=b2-4ac >0 vuol dire che l'equazione ha due soluzioni
reali e distinte x1 ed x2 che rappresentano l'intersezione
della curva descritta dal trinomio di secondo grado (la parabola) con l'asse delle x e il
segno della disequazione č rappresentato dal seguente grafico:
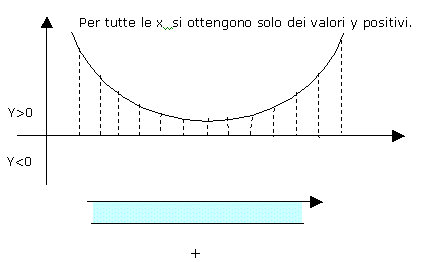
2) se D=b2-4ac
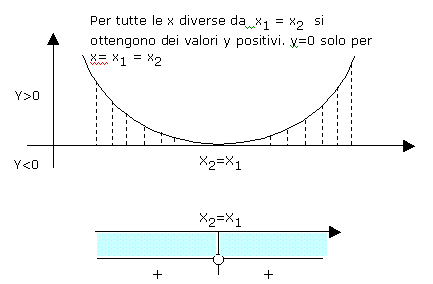
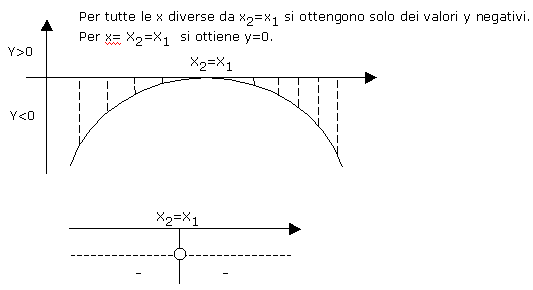
=0 vuol dire che l'equazione ha due soluzioni reali e coincidenti x1 =
x2 che rappresentano il punto di contatto della curva con l'asse delle x ed il
trinomio risulta essere sempre positivo eccetto nel punto x1 in cui si annulla
(il segno del trinomio č concorde con il segno del termine a). Graficamente questa
situazione si rappresenta nel modo seguente: vuol dire che l'equazione ha due soluzioni reali e coincidenti x1 =
x2 che rappresentano il punto di contatto della curva con l'asse delle x ed il
trinomio risulta essere sempre positivo eccetto nel punto x1 in cui si annulla
(il segno del trinomio č concorde con il segno del termine a). Graficamente questa
situazione si rappresenta nel modo seguente: