Vincenzo Calabrò
(Docente di Fisica e Laboratorio presso il Liceo-Ginnasio “B.Russell” di Roma)
http://users.libero.it/v.calabro
UN CASO DI “PROBLEM SOLVING” DI FISICA :
la risoluzione di un problema di urto elastico in un triennio di liceo scientifico.
Premessa
Il problema che qui presento come esempio di risoluzione di un problema di fisica è degno di attenzione per diverse ragioni. Intanto, è un esempio concreto e interessante che riguarda la vita reale dei giovani nel mondo dello sport. Si tratta di un sistema di corpi costituiti da due "oggetti" che hanno molta visibilità nel mondo dello sport giovanile di massa. Un pallone di pallacanestro è spesso adoperato in quasi tutte le palestre delle scuole d’Italia ad essere veicolo di movimento e di sport. Un po’ meno, in verità, una palla di baseball, perché l’Italia non è gli USA, dove questo sport spopola per interesse e passione. In secondo luogo, perché è un fenomeno facilmente riproducibile e, pertanto, soggetto a possibile “conferma empirica”. In terzo luogo, perché impone agli studenti uno sforzo di forte concentrazione mentale per visualizzare bene nella propria mente la corretta evoluzione del fenomeno. Com’è noto, uno dei motivi statisticamente più rilevante di insuccesso degli studenti nella risoluzione di un problema di fisica è dovuto alla superficiale lettura del testo che essi fanno, con la conseguenza che l’evoluzione del fenomeno non è da loro compresa bene. Insomma, gli studenti sbagliano spesso a risolvere un problema perché non lo hanno ben inteso. Sembrerà paradossale ma è così. Molti studenti leggono il testo velocemente e in maniera acritica, si precipitano subito sul foglio a fare calcoli e a scrivere mnemonicamente formule e relazioni matematiche senza avere in mente con chiarezza una traccia di percorso risolutivo, nè di come evolve il fenomeno e, al limite, senza aver capito bene quali sono le incognite da calcolare. Questo problema, e molti altri presenti nel manuale dei proff. Halliday, Resnick e Walker, si sforza di dare un esempio di comprensione del testo e di successiva applicazione del metodo del "problem solving" in maniera “indolore” secondo una traccia semplice ed efficace. In breve, il consiglio che posso dare è di leggere il testo più volte per comprenderne il senso. In questa fase non è necessario usare penna e quaderno. Anzi, è preferibile non adoperarli per niente e concentrarsi, mentalmente, a pensare al fenomeno e a come evolve nel tempo. Insomma, fare mente locale - come si vede spesso in televisione con la moviola - al fenomeno rallentato, cercando di "vedere" il percorso degli oggetti in moto e associando loro valori delle grandezze fisiche caratteristiche (compresa la loro vettorialità) che ne possano descrivere efficacemente la loro rappresentazione fisica. In questa fase è necessario porsi delle domande relative al "perchè" e al "come" di quella traiettoria, immaginando quali possano essere le cause di una alterazione del moto e individuando possibili punti di maggior interesse fisico nella evoluzione del fenomeno stesso ai quali associare valori ben definiti, sebbene in questa fase solo qualitativamente, delle grandezze fisiche che interessano il fenomeno. Osservazione importante sembra essere, infine, quella di dare nulla per scontato. Se pallone di pallacanestro e palla da baseball si scontrano chiedersi subito e perchè se si tratta di urto elastico o anelastico. Giustificare sempre le risposte. In base alla risposta tenere conto che si dovranno utilizzare i principi di conservazione della q.d.m. e dell'energia in un modo o in un altro. Si prega il lettore interessato a seguire con ordine e attenzione tutti i successivi passaggi della risoluzione. Ultimo motivo per cui lo si intende un buon “esemplare” da mostrare come modello è che in realtà esso è un “doppio problema”, nel senso che riguarda sia un quesito, sia un problema. E' pertanto possibile approfondire il fenomeno e il metodo di risoluzione. Inizieremo lo studio del fenomeno risolvendo prima il quesito e subito dopo il problema.
Quesito 10 (p.212)
|
Dall’altezza della spalla lasciate cadere, successivamente, una palla da baseball e un pallone da pallacanestro su un pavimento duro, e osservate a quale altezza rimbalzano. In seguito mettete la palla verticalmente sopra il pallone, tenendoli appena separati come indicato in figura e lasciateli simultaneamente cadere. (a) L’altezza di rimbalzo del pallone è ora maggiore o minore di prima? (b) L’altezza di rimbalzo della palla da baseball è maggiore o minore della somma dei due rimbalzi di palla e pallone? |
|
|
ANALISI DEL FENOMENO
Prima fase: Pallone M e palla m
Nel primo caso previsto dal testo del quesito i due corpi lasciati cadere liberamente da una certa altezza h rimbalzano sul pavimento duro e raggiungono praticamente la stessa altezza. Nella realtà, piccole differenze nell’altezza di rimbalzo possono verificarsi in ragione della diversa composizione del materiale di cui sono formati i due corpi e del differente grado di elasticità nel rimbalzo. Da un punto di vista teorico, cioè del modello teorico di due punti materiali semplificato dalle complicazioni della resistenza dell’aria e dell’urto non perfettamente elastico con il pavimento, l’altezza raggiunta nel rimbalzo è la stessa per entrambi i corpi. Infatti, l’altezza h raggiunta non dipende, né dalla massa, né dal volume delle due palle ma solo dalla velocità iniziale al suolo dei due corpi che dipende solo dall’altezza di caduta e dall’accelerazione di gravità. Con simbolismo matematico appropriato possiamo scrivere che h = f(h,g). Infatti, per entrambi i corpi di massa differente il calcolo prevede l’uso del principio di conservazione dell’energia meccanica nei due stati iniziale (altezza h) e finale (al suolo):
E = Ui + Ki = Uf + Kf = cost.
m g h = ½ m vm2 M g h = ½ M vM2
vm = √ 2gh vM = √ 2gh .
in entrambi i casi. Dunque, i due corpi arrivano al suolo con la stessa velocità, colpiscono il pavimento e vengono rimbalzati verso l’alto con la stessa velocità, raggiungendo alla fine la stessa altezza di rimbalzo.
Seconda fase:
- Pallone M
Il pallone M, dopo l’impatto nella caduta con il pavimento, ha appena il tempo di rimbalzare che gli “piove” addosso dall’alto la palla m che lo segue a breve distanza subendo un urto elastico. Per il principio di conservazione della q.d.m. il pallone M scambia nell’urto elastico alla palla m, a suo svantaggio, una certa q.d.m., rallentando la sua corsa verso l’alto fino a fermarsi e diminuendo conseguentemente la sua altezza di rimbalzo. L’altezza raggiunta dal pallone M, pertanto, è molto piccola. La risposta alla domanda (a) pertanto è che l’altezza di rimbalzo del pallone è minore.
- Palla m
La palla m al contrario subendo un urto elastico verso l’alto prodotto dal pallone di massa M>>m acquisisce nel rimbalzo una q.d.m. a suo favore che le permette di muoversi con forte velocità verso l’alto decisamente maggiore di quella del pallone M, raggiungendo un’altezza di rimbalzo molto maggiore della somma dei due rimbalzi precedenti e separati di pallone e palla. La risposta alla domanda (b) pertanto è che l’altezza di rimbalzo della palla è più grande.
CONSIDERAZIONI CRITICHE E STIMA DEI VALORI PIÚ PROBABILI
In relazione alle stime dei valori dei parametri fisici che intervengono nel moto del sistema (pallone-palla-altezza del soffitto-altezza della spalla dell’osservatore) si può supporre con ragionevole certezza che in una stanza alta circa 3,0 m se si lasciano cadere contemporaneamente come prevede il testo del quesito, un pallone da pallacanestro di circa 0,600 kg e una palla da baseball di circa 0,200 kg dall’altezza della spalla di un normale osservatore alto circa 1,80 m (spalla alta circa 1,50 m dal suolo) e supponendo che l’urto sia di tipo elastico, le leggi di conservazione della q.d.m. e dell’energia cinetica ci informano che la palla m arriva a fermarsi, probabilmente, in prossimità del soffitto della stanza. Il quesito posto dall’Autore del testo ha il significato di far comprendere allo studente che il risultato relativo alla diversità di altezza raggiunta nel rimbalzo dal pallone e dalla palla è dovuto alla differenza della massa dei due oggetti protagonisti del rimbalzo, perchè M>>m, confermando l’aspettativa che si può aumentare o diminuire la q.d.m. p di un corpo agendo sia sulla massa sia sulla velocità nella formula di definizione p = m v . Pertanto, un urto elastico (supposizione del modello teorico di fenomeno, sfrondato cioè dalla complessità degli attriti che inevitabilmente intervengono nella realtà) che soddisfa la validità dei due principi di conservazione della q.d.m. p e dell’energia cinetica K, conferma e giustifica la differenza di comportamento dei due corpi di massa differente.
Problema 37P (p. 216)
|
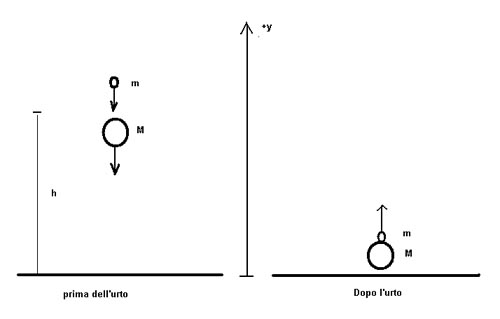
Una palla di massa m è tenuta esattamente sopra un’altra di massa M a piccola distanza, come in figura). Entrambe vengono lasciate cadere contemporaneamente da un’altezza h (ammettiamo che i loro raggi siano trascurabili rispetto all’altezza h). (a) Se M rimbalza elasticamente dal suolo e poi m rimbalza elasticamente da M, per quale rapporto m/M si vedrà M bloccarsi dopo lo scontro con m? (Il risultato corrisponde all’incirca al rapporto fra le masse di una palla da baseball e di un pallone da pallacanestro, come ne quesito 10. (b) Che altezza poi raggiunge m? |
 |
ANALISI DEL FENOMENO
Pallone M e palla m che cadono contemporaneamente.
La prima cosa da fare quando ci sono corpi in moto è individuare un sistema di riferimento in grado di dare senso cinematico al moto dei corpi. In particolare, visto che il moto è verticale, cioè secondo la direzione che unisce i corpi e il centro della Terra ci interessa individuare un verso positivo sull’asse delle ordinate, ovvero all’sull'asse delle y. Scegliamo il verso positivo diretto verso l’alto: quindi una velocità verso il basso è negativa, mentre una velocità verso l’alto è positiva. Questo è un punto molto importante della logica del "problem solving" (in generale) e del processo mentale di analisi del moto rallentato (in particolare) che deve essere compreso dallo studente senza ambiguità e superficialità di sorta. Una negligenza o, peggio, una sua sottovalutazione porterà ad attribuire sempre in maniera nefasta un segno opposto a una velocità in un'equazione, con conseguenze disastrose sul piano dei risultati. Calcoliamo adesso la velocità posseduta da pallone e palla quando si urtano elasticamente. Analizziamo il moto dei due corpi. All’inizio, liberati contemporaneamente in aria si muoveranno sotto l’effetto della gravità, entrambi verso il basso. Ma il pallone che è più vicino al pavimento arriva prima al suolo. Rimbalza e inverte il moto, iniziando la risalita. Ma in quel momento arriva, sfasata della distanza iniziale fra i due corpi, la palla in moto verso il pavimento che collide elasticamente con il pallone urtandolo dall’alto verso il basso. La domanda (a) del testo del problema chiede di calcolare dopo l’urto elastico per quale rapporto m/M si vedrà M bloccarsi dopo lo scontro con m. Prima di applicare il principio di conservazione della q.d.m. all’urto tra palla e pallone conviene calcolare le velocità possedute dai due corpi all’inizio dello scontro. Ricordiamo che M sta salendo mentre m sta scendendo. Prevediamo dunque che la velocità di M sia positiva perché diretta concordemente verso l’alto con il verso positivo dell’asse delle ordinate, mentre la velocità di m è negativa. Applichiamo il principio di conservazione dell’energia meccanica a uno solo dei due corpi, per esempio alla massa m. Si avrà: m g h = ½ m v2 . Semplificando m in entrambi i membri (perché si dividono entrambi i membri per m che è diversa da zero) avremo v= √2gh , cioè v1i = - √2gh . Per M avverrà la stessa cosa perché, com’è noto, la velocità di un corpo in caduta libera non dipende dalla massa ma solo dall’altezza e dal valore dell’accelerazione di gravità in quel punto. Pertanto per M si avrà v2i = + √2gh . In queste condizioni ci immaginiamo un modello di moto evidenziatola due velocità iniziali rappresentate da due vettori verticali e discordi.
Pallone M e palla m si scontrano mediante un urto.
L’urto è elastico. Lo afferma il testo del problema. E’ dunque un dato. Pertanto, se si applicano i due principi di conservazione della q.d.m. e dell’energia cinetica nel caso di urto elastico con bersaglio mobile si avrà:
m1 v1i +m2 v2i = m1 vif + m2 v2f
½ m1 v21i +1/2 m2 v22i = ½ m1 v2if + ½ m2 v22f
Mettendo a sistema le due equazioni abbiamo un sistema di due equazioni in due incognite che risolto dà:
 |
Prendiamo in considerazione la seconda equazione perché si tratta di una relazione che permette di calcolare il valore della velocità finale posseduta dal pallone dopo l’urto. Questa velocità come dice il testo del problema è zero, perché il pallone si vedrà bloccato come conseguenza dell’urto con la palla. Dunque v2f = 0. L’equazione (2) diventerà:
Sviluppando i passaggi si otterrà:
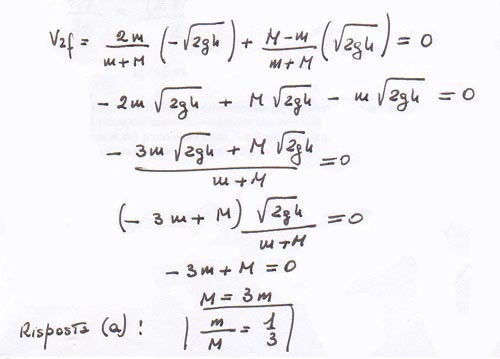 |
La risposta (a) ci informa che il rapporto tra le masse è uguale a 1/3, che è come dire che la massa M del pallone è 3 volte più grande della massa m della palla. Se andiamo a misurare le masse di un pallone da pallacanestro e di una palla da baseball in effetti si ottengono valori intorno a M=600 g e m=200g, confermando la bontà del calcolo effettuato.
Dopo l’urto elastico che altezza h raggiunge la massa m dal suolo?
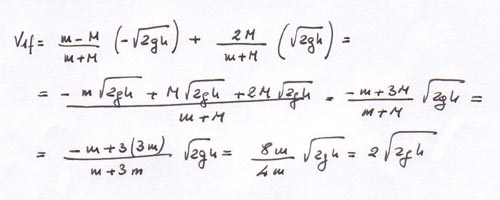 |
Per calcolare la massima altezza raggiunta dalla palla, che indicheremo con H, è opportuno utilizzare la formula v2=vo2 – 2 a x. Sostituendo i simboli del problema avremo:
0 = v21f – 2 g H,
da cui:
v21f = 2 g H e dunque:
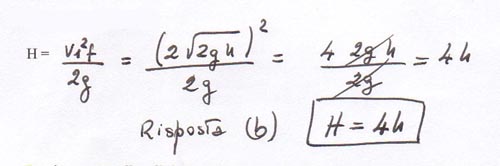 |
Possiamo controllare il risultato della risposta (b) mediante una via alternativa di carattere cinematico. Proviamo a rifare dei nuovi ragionamenti che non utilizzano i principi di conservazione ma solo le equazioni orarie del moto della palla. Vedremo che la previsione ottenuta sopra sarà confermata in pieno . Infatti dalla relazione v2 = vo2 – 2 a x
Dove v è la velocità finale della palla alla massima altezza dove si ferma con velocità nulla. Dunque v=0, dove vo è la velocità iniziale della palla subito dopo l’urto con il pallone. Questa velocità l’abbiamo chiamata vif=2 √ 2gh . Pertanto 0 = v2if – 2 g H ovvero 0 = (2 √ 2 g h)2 – 2 g H che dà H = 4 2 g h /2g = 4 h . c.v.d.
STIMA DEI VALORI PIÚ PROBABILI
Anche qui, come ne quesito Q10, in relazione alle stime dei valori dei parametri fisici che intervengono nel moto del sistema (pallone-palla-altezza della palla) si può supporre con ragionevole certezza che in una stanza alta circa 3,0 m se si lasciano cadere contemporaneamente come prevede il testo del quesito un pallone da pallacanestro di circa 0,600 kg e una palla da baseball di circa 0,200 kg dall’altezza della spalla di un normale osservatore alto circa 1,80 m (spalla alta circa 1,50 m) e supponendo che l’urto sia di tipo elastico, le leggi di conservazione della q.d.m. e dell’energia cinetica ci permettono di calcolare facilmente i valori delle velocità prima dell’urto e immediatamente dopo l’urto. Ecco di seguito il calcolo.
Le due velocità iniziali dei due corpi sono le stesse. Lo abbiamo già visto nel caso del Q10.
v1i = v2i = √2gh = √ 2 9,8 1,50 = 5,4 m/s.
v1f = [(m-3m)/(m+3m) (-5,4) + (2 3m)/(m+3m) (5,4)] = -1/2 (-5,4) + 3/2 (5,4) = 10,8 m/s
v2f = [(2m)/(m+3m) (-5,4) + (3m-m)/(m+3m) (5,4)] = -1/2 (5,4) + 1/2 (5,4) = 0
Dunque, la velocità finale della palla in salita è il doppio di quella che aveva prima nella discesa, mentre la velocità del pallone è zero, che conferma la validità delle affermazione fatte nel testo.
Descrizione sintetica della risoluzione del problema
|
A seguire, riporto una descrizione sintetica della risoluzione del problema. Di solito gli studenti prediligono questa forma di comunicazione, che non presenta alcuna comunicazione sottoforma di idee, di ragionamenti, di spiegazioni fisiche e, viceversa, esalta quasi esclusivamente la successione dei passaggi matematici in forma algebrica. Questo modo di concepire la risoluzione di un problema di fisica, ricorda molto il cosiddetto "compito scritto di matematica" in cui è esaltata soltanto la dimensione del formalismo matematico a scapito delle idee fisiche. Ripeto, che in questa maniera gli studenti fanno torto alla loro intelligenza, perchè il ritenere che nella risoluzione di un problema di fisica sia sconveniente intercalare a passaggi matematici considerazioni fisiche relative ai vari momenti della risoluzione è un modo riduttivo e limitato di considerare il "problem solving" solo come palestra di matematica. E male fanno quegli insegnanti che non riprendono gli studenti su questo tema e non fanno nulla per far capire loro che le scienze fisiche e le altre scienze, sono discipline che hanno tutte un alto valore culturale e formativo. |
||
|
|
||
|
|
||
Conclusioni
Il problema 37P e il quesito Q10 mostrano in modo opportuno l’efficacia sorprendente dell’uso incrociato dei principi di conservazione della q.d.m. e dell’energia cinetica negli urti elastici. In pratica le due leggi sono in grado di calcolare il risultato dinamico di un qualsiasi urto che si ottiene come processo di calcolo delle velocità finali dei due corpi dopo la collisione elastica. Non sembri retorico affermare che i principi di conservazione in fisica, se adeguatamente utilizzati, sono in grado di risolvere qualsiasi problema che abbia a che fare con lo scontro fra due oggetti, in modo sintetico e adeguato, a condizione che si possa fare una netta distinzione fra istanti prima, durante e dopo la collisione.