Proprietà meccaniche
Elasticità
Un corpo soggetto alla azione di una forza subisce una deformazione, se questa tuttavia regredisce completamente dopo che l’azione della forza è terminata allora il corpo è detto idealmente elastico. In questo caso esso è soggetto alla legge di Hooke per la quale la deformazione D è proporzionale alla forza applicata (stress S) mediante una costante M detta modulo:
![]()
a seconda del tipo di deformazione si distinguono tre tipi di moduli
è relativo ad una deformazione e causata da una forza di trazione o stiramento è anche detto modulo di Young: ![]()
detto anche modulo trasversale di elasticità o modulo di torsione (figura 1), è relativo ad una deformazione t causata da una forza di taglio g ![]()
è relativo ad una deformazione causata da una compressione isostatica.
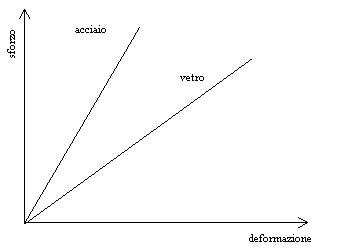
Nella figura 2 è riportata la relazione tra sforzo e deformazione, il modulo è rappresentato dallo slope della retta.
Lo sforzo s è definito come una forza P per unità di superficie A (Cauchy) ovvero ![]() , in figura 1 è mostrata una deformazione a seguito di uno sforzo di taglio , la deformazione g è in questo caso definita dall’angolo di deformazione in radianti causato dallo sforzo t.
, in figura 1 è mostrata una deformazione a seguito di uno sforzo di taglio , la deformazione g è in questo caso definita dall’angolo di deformazione in radianti causato dallo sforzo t.
Figura 1 : sforzo di taglio

Se ad esempio consideriamo il modulo di Young od elastico, un valore piccolo significa che un piccolo sforzo provoca una deformazione grande (materiale flessibile) mentre un valore del modulo grande significa che piccole deformazioni sono prodotte da grandi sforzi (il materiale è rigido), E(vetro)= 70.000 MPa, E(acciaio)= 210.000 MPa, E(gomma)= 7 MPa. (1 MPa=10,2 Kg/m2 = 1MN/m2).
Figura 2 diagramma sforzo-deformazione
Nella deformazione avvenuta in seguito ad una forza di trazione applicata ad un campione si registra una contrazione in una direzione normale a quella su cui è applicata la forza di tensione. Se la deformazione relativa è ![]() e la contrazione trasversale è
e la contrazione trasversale è ![]() dove l è la lunghezza del provino e d lo spessore , allora si può definire un rapporto di Poisson m tale che:
dove l è la lunghezza del provino e d lo spessore , allora si può definire un rapporto di Poisson m tale che:
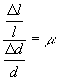
Figura3 : deformazioni indotte da uno sforzo di trazione
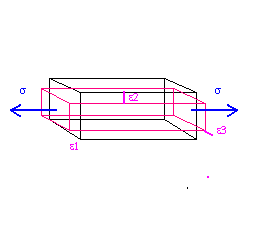
Nelle tre dimensioni (figura 3) se consideriamo le deformazioni lungo la direzione dello sforzo e1 e quelle lungo gli assi perpendicolari e2 ed e3 esse stanno tra di loro secondo il rapporto di Poisson:
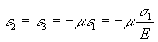
indicativamente questo rapporto varia nei vetri tra 0,15 e 0,26.
I tre moduli prima citati sono legati tra di loro attraverso m :
![]()
Poiché E e K sono sempre positivi il valore massimo che m può assumere è 0,5: in questo caso K assume il valore zero come nei liquidi che sono incomprimibili.
Metodi di misura
1.2.1) Metodo a flessione
se fissiamo un cilindro di vetro di lunghezza l e di raggio r ad una estremità e misuriamo la flessione h che esso subisce sotto un carico P possiamo ricavare in modulo di elasticità E con la seguente relazione:
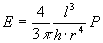
1.2.2) Metodo delle vibrazioni
una fibra di vetro di densità r e lunghezza l note è messa in vibrazione da un generatore di onde ultrasoniche. Se la fibra di vetro vibra nel modo fondamentale (un solo nodo in mezzo al campione) e con vibrazioni longitudinali allora il modulo elastico E è dato:
![]()
dove n è la frequenza di vibrazione. E’ un metodo indipendente dalla sezione del provino.
1.2.3) Metodo a torsione
Applicando una forza di torsione M ad un filamento di vetro di raggio r e lunghezza l a cui è stata fissata una estremità si può calcolare il modulo di taglio G con la seguente relazione:
![]()
dove a è la misura dell’angolo di torsione della fibra espressa in radianti.
1.2.4) Metodo della massa inerziale
in questo caso al filamento di vetro di raggio r viene applicata ad una estremità una massa con un momento di inerzia J, se t è il periodo di una vibrazione del filamento l la lunghezza ed r il raggio si ha:
![]()
1.2.5) Metodo della propagazione di ultrasuoni
Il modulo di compressione K si ricava sfruttando la propagazione di ultrasuoni nella massa del campione:
![]()
dove u è la velocità di propagazione degli ultrasuoni nel campione di vetro e r la densità. Con questo metodo si può facilmente misurare la compressibilità k dei vetri: ![]() inoltre questo è un ottimo metodo per misurare eventuali stress all’interno di oggetti non trasparenti.
inoltre questo è un ottimo metodo per misurare eventuali stress all’interno di oggetti non trasparenti.
1.2.6) misura del rapporto di Poisson m
una misura sperimentale del rapporto di Poisson può essere eseguita valutando la curvatura di un provino di vetro modellato come una striscia e sottoposto ad un carico. Se a è l’angolo tra gli asintoti allora
![]()
Dipendenza del modulo elastico dalla composizione chimica
Un campione di vetro se sottoposto ad una forza di trazione subisce un allungamento nella direzione in cui questa forza viene applicata , il modulo elastico E è inversamente proporzionale a questo allungamento. Tanto maggiore è E tanto più rigida sarà la struttura chimica del vetro ovvero tanto minore sarà il numero degli ossigeni non a ponte.
Da queste considerazioni è evidente che la SiO2 vetrosa deve possedere un alto modulo di Young (720 Kbar) [1Kbar = 108 N/m2].
Il vetro di B2O3 possiede una struttura più aperta di quella della silice fusa, esso ha un modulo elastico molto più basso ( E=175 Kbar) tuttavia con l’aggiunta di ioni alcalini si ha un aumento del modulo fino anche a 600 Kbar a causa dell’irrigidimento della struttura dovuto alla coordinazione tetraedrica del boro. Questo andamento presenta un massimo per poi diminuire a concentrazioni superiori di alcali a causa del cambiamento di coordinazione del boro [BO4] ® [BO3]. (Anomalia del boro).
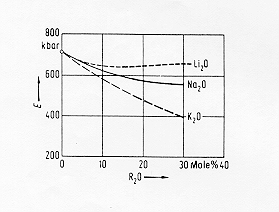
L’introduzione di ossidi di metalli alcalini in un vetro di silice fa aumentare il numero degli ossigeni non a ponte della struttura e quindi provoca un abbassamento del modulo elastico (figura 4)§ 7.2a
Come vediamo dalla figura questo abbassamento sarà meno marcato per lo ione Li+ ( forza di campo maggiore e quindi più polarizzante degli ioni Na+ e K+ ) di quanto non lo sia per gli altri elementi alcalini.
Anche i metalli della transizione, a causa della loro polarizzabilità, manifestano per aggiunte progressive in vetri silicatici una tendenza simile a quella dei metalli alcalini.
Per quanto riguarda l’effetto del Al2O3 e B2O3 in vetri alcalino-silicatici il loro effetto è quello di un aumento di E all’aumentare della loro concentrazione a causa della loro propensione a coordinare ioni alcalini e quindi a togliere ossigeni non a ponte con la formazione di gruppi [AlO4] e [BO4] (vetro allumino-silicatico: E = 910 Kbar).
Figura 4 § 7.2a
Dipendenza della compressibilità dalla composizione chimica
Come abbiamo visto nel modello strutturale della silice fusa questa possiede una struttura piuttosto "aperta" quindi ha una compressibilità, k definita come l’inverso del modulo di compressione 1/K, elevata (2,7 10-6 Bar), come vediamo in figura 5 § 7.2b con l’aggiunta degli ioni alcalini le lacune nella struttura vengono progressivamente colmate e si osserva quindi un decremento della compressibilità k.
Figura 5
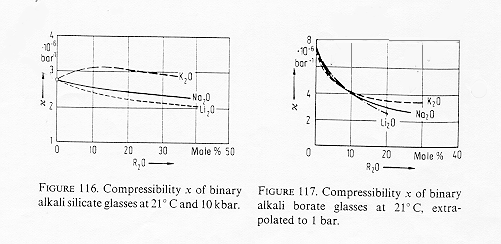
In questo caso l’ordine tra i metalli alcalini è invertito e addirittura nel caso del K+ si ha un leggero aumento della compressibilità, questo fenomeno è spiegabile con il fatto che ioni di raggio molto elevato come il K+ sono più facilmente deformabili di ioni di piccolo raggio come Li+.
L’equilibrio tra i due effetti di riempimento delle lacune nella struttura del vetro e di deformabilità dei cationi si vede bene nel caso di vetri alcalino-boratici: a bassi tenori di alcali la compressibilità è guidata dal processo di riempimento delle lacune strutturali che saranno riempite in maniera più efficace da cationi di elevato raggio: la diminuzione della curva della compressibilità avviene nella serie K2O > Na2O >Li2O. Con elevati tenori di alcali prevale invece l’effetto della deformabilità del catione che è più accentuata,come si è detto, per quelli di largo raggio ionico.
Modelli matematici
Anche in questo caso possiamo considerare il modulo di elasticità E una proprietà additiva dei vetri vari autori hanno proposto dei coefficienti empirici validi per un certo numero di componenti del vetro l’equazione proposta da Winkelmann e Shott è la seguente:
![]()
dove Ei è il contributo di ogni singolo componente al modulo elastico totale e pi è la frazione molare percentuale.
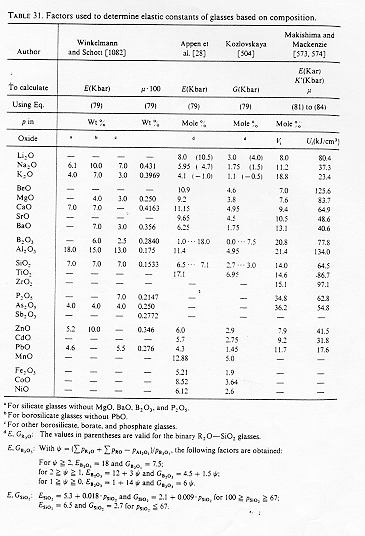
Makishima e Mackenzie hanno proposto un’altra equazione partendo dal presupposto che il modulo elastico sia in relazione diretta con l’energia di dissociazione di legame U e con la densità di impacchettamento atomico Vt, a sua volta la densità di impacchettamento è proporzionale attraverso un fattore empirico Vi alla frazione in peso dei rispettivi componenti il vetro:
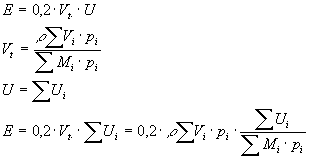
dove Mi è il peso molecolare e r è la densità, sostituendo a Vi e Ui i rispettivi coefficienti si può calcolare il modulo di Young di un vetro. In figura 6 § 7.3 sono riportati i fattori per la determinazione delle costanti elastiche nei vetri a partire dalla loro composizione.
Figura 6
Dipendenza del modulo elastico dalla temperatura
All’aumentare della temperatura le forze di legame interatomiche in un vetro si indeboliscono si assiste pertanto ad un abbassamento del valore del modulo elastico (e di quello di rottura), il valore del modulo subisce poi alla temperatura di transizione vetrosa un brusco decremento come illustrato in figura 7.
Figura 7
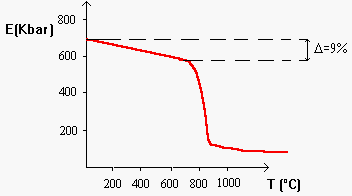
Il decremento del modulo di elasticità dipende anch’esso dalla composizione del vetro, in genere maggiore è il contenuto in SiO2 e più piccolo è il delta, per un vetro di silice pura il valore è circa del 9%.
Come vediamo dalla figura 1 anche per le proprietà meccaniche è importante la storia termica del vetro ad esempio vetri raffreddati rapidamente presentano moduli elastici ed in genere proprietà meccaniche inferiori a vetri tenuti in annealing ad una temperatura di poco inferiore a quella della transizione vetrosa. Un esempio è rappresentato da un vetro da finestra sodico-calcico-siliceo il quale se raffreddato rapidamente ha un modulo di elasticità di 715 Kbar inferiore al valore raggiunto dal medesimo vetro tenuto per 1 h alla temperatura di 700° cioè di 745 Kbar.
Resistenza alla frattura
Si deve distinguere tra una resistenza teorica ed una resistenza sperimentale le quali differiscono a causa dell’influenza di svariati fattori come la storia termica del vetro, la presenza di difetti superficiali ecc.
Resistenza teorica (secondo Griffith)
Essa è unicamente determinata dalla forza dei legami interatomici questo assunto è vero in assenza di difetti. La resistenza teorica viene definita come il lavoro necessario per creare nuova superficie in conseguenza di una frattura.
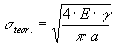
dove E è il modulo elastico, g è l’energia libera superficiale ed a è la distanza interatomica. Per i vetri silicatici s teor = 1,3 1010 N/m2 ed è approssimativamente circa ![]() del modulo elastico E.
del modulo elastico E.
Resistenza sperimentale
E’ di diversi ordini di grandezza inferiore alla resistenza teorica: ad esempio in vetri sodio-calcio-silicatici la resistenza alla trazione è circa 5 107- 2 107 N/m2. Essa è influenzata dalla forma del campione: ad esempio la resistenza a trazione s per le fibre di vetro varia 170 MN/m2 per quelle con un diametro di 1 mm a 3400 MN/m2 per diametri di 3 m m. Anche la storia termica del vetro influenza la sua resistenza: infatti raffreddamenti troppo rapidi portano in genere a lacune strutturali e quindi a strutture meno rigide e più aperte: per ottenere vetri con alte resistenze si devono utilizzare industrialmente basse velocità di trafilatura o di scorrimento in modo che il raffreddamento sia il più lento possibile. Il fuso deve essere tenuto ad una viscosità piuttosto alta prima di essere lavorato e raffreddato in questo modo ci si assicura elevate resistenze nei vetri finiti.
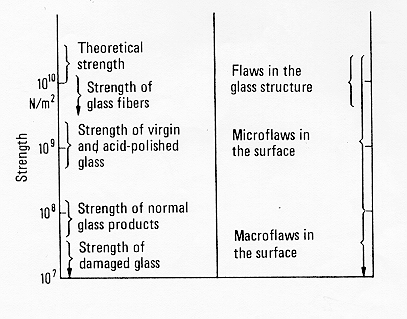
Generalmente viene osservato che la resistenza delle fibre di vetro diminuisce all’aumentare della loro lunghezza così come la resistenza delle lastre piane diminuisce all’aumentare della superficie questo fenomeno è in relazione con la presenza di microfratture superficiali. Come vedremo più avanti questi difetti possono essere eliminati con trattamenti termici o chimici (politura con HF), in figura 8 § 7.5 si vede un riassunto schematico della resistenza dei vetri in relazione a microdifetti superficiali.
Le microfratture si mettono in evidenza per mezzo di una deposizione di vapori di sodio (Adams-Mc Millan) oppure per immersione del vetro in esame per 15’ a 250° in un bagno di sali fusi LiNO3-KNO3, (Ernsberger) in questo caso si creano delle tensioni superficiali a causa dello scambio ionico del Na+ con K+ e Li+ che rendono visibili le fratture altrimenti invisibili.
Figura 8 § 7.5
Frattura del vetro
Il vetro è un materiale fragile cioè la frattura avviene senza essere preceduta da una apprezzabile deformazione plastica, a livello atomico questo significa che la frattura avviene per distacco dei piani atomici contigui con completa separazione tra gli atomi.
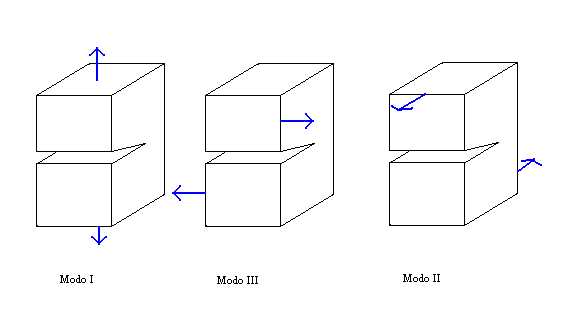
Secondo la trattazione classica di Inglis, Griffith, Irwin si considera che il processo di frattura avvenga in un continuo elasticamente lineare ed isotropico in tal senso si può parlare di meccanica della frattura elastico-lineare. Gli stress coinvolti sono molto complessi ma possono essere ricondotti alla sovrapposizione di tre tipi fondamentali (figura 9):
1) modo I : apertura della fessura su di un piano perpendicolare alla direzione di applicazione della forza.
2) modo II : apertura della fessura su un piano parallelo alla direzione di applicazione della forza.
3) modo III : frattura trasversale o antiplanare.
per semplicità il modello I.G.I considera solo fratture del tipo I
Figura 9
La frattura fragile ha due importanti caratteristiche:
Nel 1920, Griffith fece l’ipotesi che la frattura nei materiali fragili ed in particolare nel vetro fosse imputabile alla presenza di microscopiche fratture sulla superficie. Per questa ragione il valore della resistenza reale del vetro risultava molto inferiore a quello della resistenza teorica.
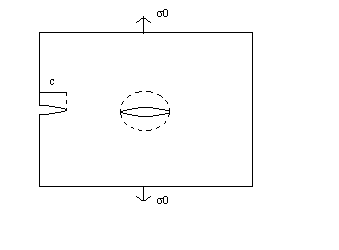
La presenza di microfratture indebolisce il materiale poiché una sollecitazione anche modesta viene amplificata in corrispondenza delle estremità delle cricche causandone la propagazione e quindi la rottura del materiale stesso.
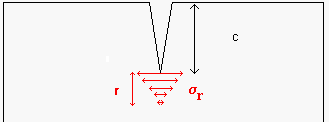
Supponiamo che una sollecitazione unitaria di trazione s0 sia applicata ad una lastra sottile contenente al suo interno una fenditura ellittica di lunghezza 2c e raggio di curvatura r (al vetrice), che la tensione s0 agisca perpendicolarmente all’asse maggiore della fenditura ( modo I) e la lastra si possa considerare di dimensioni infinite (rispetto a quelle della fessura).
In corrispondenza dell’apice della fenditura si ha una concentrazione delle tensioni il cui valore massimo, ammettendo che c>>r , è dato da:
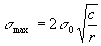 1
1
La tensione s0 applicata in modo uniforme viene quindi amplificata all’apice della frattura di un fattore ![]() .
.
Le microfratture in un vetro sono lunghe in media da 0,1 mm a 10 mm mentre l’apice può avere un raggio effettivo dell’ordine delle dimensioni atomiche (alcuni Å) quindi sostituendo questi valori nella espressione sopra riportata vediamo che il fattore di concentrazione degli sforzi può variare da 100 a 1000.
Sforzi anche molto meno intensi di quelli teorici ma localizzati al vertice delle microfratture possono innescare con facilità la propagazione della cricca provocando la frattura del materiale.
La meccanica della propagazione della frattura determina la rottura progressiva dei legami atomici al vertice della frattura stessa : il fattore di concentrazione degli sforzi aumenta congruentemente alla propagazione della fessura e questo determina una sempre più facile e veloce propagazione della cricca (fino ad una velocità paragonabile a quella del suono nel materiale in oggetto).
Per avere una frattura occorre che la tensione massima smax all’apice della fessura raggiunga il valore della tensione critica di decoesione scr .
Figura 10 microfratture alla superficie di una lastra sollecitata a trazione (Modo I)
Il calcolo di scr e quindi della resistenza teorica alla frattura di un materiale si basa sulla conoscenza delle forze interatomiche e più in particolare sulla resistenza che i piani atomici oppongono ad una loro permanente separazione, la tensione critica di decoesione si può quindi calcolare in base allo sforzo necessario per spostare in maniera permanente gli atomi dalle loro posizioni di equilibrio e tenendo conto che il lavoro compiuto dalla sollecitazione medesima dovrà essere sufficiente a creare due nuove superfici di frattura.
Resistenza secondo Orowan
Analizziamo la curva delle forze che si manifestano tra atomi contigui al variare della loro distanza di equilibrio (figura 11)
Fig 11 Forza interatomica per unità di area in funzione della distanza
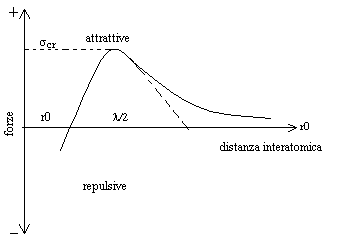
Cercando di allontanare tra loro i due atomi si sviluppa una forza attrattiva che è rappresentata dal ramo positivo della curva, questo ramo può essere approssimato ad una curva sinusoidale di passo l la cui ampiezza (forza attrattiva massima) è uguale alla forza necessaria per spostare in modo permanente gli atomi dalle loro posizioni di equilibrio, in definitiva essa rappresenta la tensione critica di decoesione.
Lo sforzo normale unitario s sarà quindi dato dalla espressione:

dove con x si intende lo spostamento. Per spostamenti molto piccoli possiamo considerare invece del seno il suo argomento e quindi l’espressione diventa:
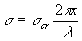 2
2
Per la legge di Hooke ![]() con e deformazione unitaria che si può considerare data dal rapporto tra lo spostamento iniziale degli atomi dalla loro posizione di equilibrio x e la loro distanza di equilibrio r0 , quindi:
con e deformazione unitaria che si può considerare data dal rapporto tra lo spostamento iniziale degli atomi dalla loro posizione di equilibrio x e la loro distanza di equilibrio r0 , quindi:
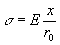 3
3
Uguagliando la 2 e la 3 si ha:
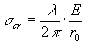 4
4
Per valutare l si consideri che il lavoro di decoesione per unità di superficie dovrà eguagliare l’energia superficiale delle due nuove superfici di frattura gs
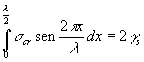
dove l’integrale della espressione sopra riportata rappresenta il lavoro compiuto dallo sforzo s. Risolvendo si ha:
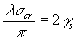 5
5
sostituendo il valore di l della 5 nella 4 si ottiene la tensione critica di decoesione ovvero la resistenza teorica del materiale espressione simile a meno di un fattore a quella data nel capitolo precedente:
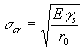
L’energia superficiale per i solidi al pari di r0 non varia molto da solido a solido e quindi la resistenza teorica è in funzione del modulo elastico E. Si può calcolare che la resistenza teorica è ![]() , ovvero i materiali idealmente fragili si rompono teoricamente a circa il 10% di deformazione unitaria, in pratica tuttavia si osserva che la maggior parte dei materiali fragili si rompe a 10-3 E ed anche meno, la frattura si ha in corrispondenza di valori circa due ordini di grandezza più bassi di quelli teorici.
, ovvero i materiali idealmente fragili si rompono teoricamente a circa il 10% di deformazione unitaria, in pratica tuttavia si osserva che la maggior parte dei materiali fragili si rompe a 10-3 E ed anche meno, la frattura si ha in corrispondenza di valori circa due ordini di grandezza più bassi di quelli teorici.
Per un vetro piano la resistenza può aggirarsi sugli 8-10 kg/mm2 (valore medio del carico di rottura a trazione da flessione) mentre nel caso di fibre di vetro del diametro di qualche micron si può arrivare a valori di 300-350 Kg/mm2 , questo a causa dell’assenza di difetti ed anche perché l’eventuale azione di quest’ultimi è resa meno efficace dallo stiramento lungo la direzione di trafilatura.
Studiando il meccanismo di frattura nei vetri, Griffith determinò le condizioni di propagazione delle microfratture supponendo che una fessura ellittica possa estendersi liberamente se questo porta ad una diminuzione dell’energia libera del sistema.
Quando una fessura inizia a propagarsi si ha un rilascio di energia elastica tuttavia una certa quantità di energia viene immagazzinata come energia superficiale dovuta alla creazione di nuova superficie.
L’energia di deformazione elastica per unità di spessore rilasciata dall’estendersi di una microfessura in una lastra sottile è data da :
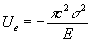
dove p c2 è il volume del cilindro di altezza unitaria che rilascia l’energia di deformazione, E è il modulo di Young e s è lo sforzo unitario applicato.
L’energia superficiale corrispondente è :
![]()
dove 2c è la lunghezza della microfessura e gs l’energia superficiale per unità di area.
La fessura si propagherà producendo frattura fragile quando ad un incremento della sua lunghezza corrisponde una diminuzione (o quantomeno nessuna variazione) dell’energia globale:
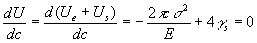
ovvero:
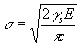
Lo sforzo necessario a causare frattura fragile è minore quando siamo in presenza di fenditure di grandi dimensioni è maggiore quando siamo in presenza di materiali con elevato modulo elastico ed alta energia superficiale.
Se ![]() le fratture tenderanno a richiudersi spontaneamente mentre quando
le fratture tenderanno a richiudersi spontaneamente mentre quando ![]() le fratture tenderanno ad aprirsi. Esiste dunque una dimensione critica della frattura
le fratture tenderanno ad aprirsi. Esiste dunque una dimensione critica della frattura ![]() come possiamo vedere in figura 12:
come possiamo vedere in figura 12:
Figura 12

dove h è l’energia di deformazione liberata nel processo di propagazione della frattura proporzionale al quadrato della lunghezza della frattura c2 mentre l’energia di frattura necessaria perché si formino cricche è proporzionale all’inverso della lunghezza delle cricche stesse 1/c
Griffith dimostrò anche che l’energia per la propagazione di una frattura fragile di questo tipo è fornita dalla energia elastica immagazzinata dalla struttura e non è quindi necessario alcun lavoro delle forze esterne.
Secondo Griffith tutti i vetri avrebbero contenuto nella loro massa una distribuzione di microscopiche fratture, di recente è stato invece dimostrato che tali cricche non sono una caratteristica intrinseca del vetro ma un fenomeno superficiale derivante da danneggiamento meccanico, da contaminazioni superficiali (ad esempio durante i trattamenti termici) o da devetrificazioni localizzate.
Le microfratture superficiali sono responsabili oltre che della fragilità, anche della bassa resistenza a trazione del vetro (8-10 kg/mm2) rispetto a quella a compressione (40-50 kg/mm2) , da questa considerazione sono stati derivati quei trattamenti termici che si fanno sui vetri per aumentarne la resistenza meccanica e che prendono il nome di tempera.
Analizzando le equazioni si vede che la sollecitazione necessaria affinchè vi sia frattura può ulteriormente diminuire se si creano le condizioni per una diminuzione della energia superficiale, ad esempio per adsorbimento di gas o fluidi che diffondono in corrispondenza dell’apice della frattura (vedi la fatica).
Nel trattare la frattura di vetri si deve anche esaminare il comportamento di questo materiale sotto sollecitazioni del tipo di quelle che possono derivare da urti improvvisi e violenti, la capacità di un vetro di resistere a carichi estremamente concentrati viene definita, sia pure in modo alquanto impreciso, come "durezza" del vetro.
La misura di questa proprietà dipende dal tipo di prova utilizzato per valutarla: nel caso del vetro si possono impiegare prove di durezza alla scalfittura, durezza alla penetrazione e durezza alla abrasione.
La resistenza all’urto di un vetro può essere valutata facendo cadere pesanti sfere di acciaio su una lastra piana appoggiata orizzontalmente, in questo caso si riscontra che l’energia necessaria per causare rottura diminuisce all’aumentare della velocità d’urto e al diminuire del diametro della sfera d’acciaio impiegata.
Per basse velocità d’urto l’energia di caduta viene completamente trasformata in energia elastica flessionale al momento della frattura (che presenta aspetto e modalità analoghe a quelle ottenibili per semplice flessione) ad alte velocità d’urto si ha invece il contributo di tensioni vibrazionali che si propagano in tutte le direzioni dal punto di impatto e si sommano alle tensioni da flessione abbassando ulteriormente la resistenza della lastra .
In quest’ultimo caso la frattura può essere di tipo "hertziano" con la formazione di un tipico cono di frattura in corrispondenza del punto di impatto.
Stress Intensity Factor
Si può assumere che per i vetri il valore r dell’equazione 1 che è decisivo per la frattura così come lo stress s0 abbiano valori costanti quindi in 1 anche il prodotto ![]() è costante, in altre parole s0 è inversamente proporzionale alla radice quadrata della lunghezza della frattura come è stato sperimentalmente confermato.
è costante, in altre parole s0 è inversamente proporzionale alla radice quadrata della lunghezza della frattura come è stato sperimentalmente confermato.
Si può allora definire uno stress intensity factor KI caratteristico di ciascun materiale e tale che:
![]()
dove s è in maniera equivalente a s 0 uno sforzo di trazione applicato esternamente. Quando s è sufficientemente alta da produrre una frattura allora si parla di critical stress intensity factor:
![]()
Si definisce una energia specifica di frattura G come l’energia necessaria per creare due interfaccie, essa è inoltre in relazione al fattore critico di stress KI, quindi per un materiale idealmente fragile:
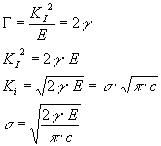
quest’ultima relazione assomiglia a quella della resistenza teorica a parte un fattore. In pratica tuttavia l’energia richiesta per il processo di frattura è considerevolmente più alta di quella teorica in quanto l’energia in eccesso viene spesa in deformazioni anelastiche al l’apice della frattura (Marsh) e per quelle reazioni chimiche irreversibili che avvengono all’apertura di una superficie di frattura fresca.
Velocità di frattura
La frattura tende inizialmente a propagarsi in modo lento e quindi raggiunge un valore massimo vB caratteristico per ciascun vetro. (vB = 1500 m/sec per i vetri silicatici , 2200 m/sec per la silice vetrosa).
Kerkof ha derivato dalla teoria molecolare una formula che dà valori sufficientemente in linea con le osservazioni sperimentali:
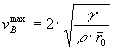
dove r0 è la distanza atomica media, per velocità più basse si nota una dipendenza di vB da KI e la velocità diventa dipendente dalla temperatura (frattura termica)e dall’adsorbimento di vapor acqueo.
Dalla figura 13§ 7.6 si vede la relazione tra la velocità di propagazione della frattura in m/sec e KI (in Nm-3/2 10-5 ) a percentuali variabili di umidità relativa. Si distinguono tre regioni:
§ 7.6
Figura 13
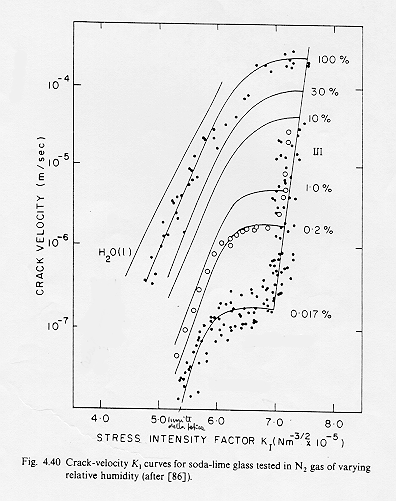
I) in questa regione detta regione di crescita subcritica della frattura guida la velocità di reazione H2O-vetro all’apice della frattura si ha un andamento lineare della velocità di frattura con KI la velocità è anche proporzionale alla percentuale di umidità relativa, L’andamento della velocità è fortemente influenzato dalla temperatura tanto che la regione I è anche detta regione della frattura termica o corrosione da stress
II) in questa seconda regione guida la velocità di diffusione dell’H2O sulla superficie della frattura e la velocità di propagazione diviene indipendente da KI mentre è conservata la dipendenza della velocità dalla percentuale di umidità relativa.
III) nella terza regione del grafico la velocità di frattura diventa troppo elevata perché la sola diffusione dell’H2O possa permettere a quest’ultima di raggiungere la neoformata superficie di frattura e quindi la velocità di propagazione ritorna proporzionale a KI. Il comportamento in questo caso assomiglia a quello di una frattura che si propaga nell’alto vuoto
Mentre il valore di KI al momento della rottura è uguale a KIC il valore di K relativo all’intersezione dell’asse X e al di sotto del quale sembra non esserci propagazione della frattura è detto limite della fatica al di sotto del quale non si ha una visibile propagazione della frattura. Misure sperimentali hanno acertato che la velocità limite massima di frattura è di 1500-2000 m/sec.
Hilling e Charles hanno ipotizzato che la corrosione da stress sia un processo termicamente attivato nel quale l’energia di attivazione Q decresce al crescere dello stress
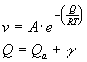 6
6
L’energia totale di attivazione è la somma dell’energia di avanzamento della frattura Qa e dell’energia superficiale g necessaria a creare nuova superficie fratturata.
La dipendenza della Qa dallo stress è definita da:
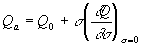
dove Q0 è una costante, quindi la (6) diventa:
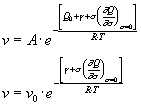 7
7
poiché ![]() è negativa Qa decresce al crescere dello stress applicato la velocità di frattura aumenta all’aumentare dello stress. L’energia superficiale g è funzione di
è negativa Qa decresce al crescere dello stress applicato la velocità di frattura aumenta all’aumentare dello stress. L’energia superficiale g è funzione di ![]() dove r è il raggio di curvatura della frattura.
dove r è il raggio di curvatura della frattura.
Come si vede dalla figura 14, in assenza di stress la velocità di corrosione è uguale sulle pareti come nel fondo della frattura, in questo caso si ha solo uno smussamento della frattura ed il rapporto ![]() tra la profondità della frattura ed il suo raggio di curvatura decresce. In presenza di stress s (figura 14b) è massima sul fondo della frattura e quindi massima sarà la velocità di frattura, mentre ai bordi lo stress e quindi la velocità di frattura sono molto bassi in questo caso
tra la profondità della frattura ed il suo raggio di curvatura decresce. In presenza di stress s (figura 14b) è massima sul fondo della frattura e quindi massima sarà la velocità di frattura, mentre ai bordi lo stress e quindi la velocità di frattura sono molto bassi in questo caso ![]() decresce. A valori più bassi di s (figura 14c) il valore di g compete con
decresce. A valori più bassi di s (figura 14c) il valore di g compete con ![]() nell’equazione (7) e la velocità di corrosione sui lati della frattura è confrontabile con quella del fondo e quindi la crepa non diventa sempre più affilata come nel caso precedente, in questo caso
nell’equazione (7) e la velocità di corrosione sui lati della frattura è confrontabile con quella del fondo e quindi la crepa non diventa sempre più affilata come nel caso precedente, in questo caso ![]() è leggermente positivo, il limite della fatica è quando s è così bassa che
è leggermente positivo, il limite della fatica è quando s è così bassa che ![]() detto stress concentration factor rimane costante e non viene rilevata propagazione di frattura.
detto stress concentration factor rimane costante e non viene rilevata propagazione di frattura.
Figura 14
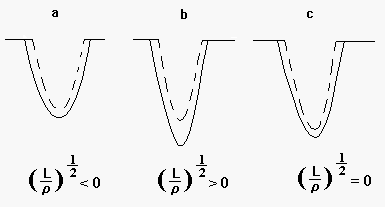
Fatica e durabilità
La velocità di crescita subcritica della frattura ha come conseguenza che in un vetro sottoposto a stress le fratture presenti sulla superficie tendono ad allargarsi finché non si arriva ad una lunghezza tipica allorché si ha una propagazione spontanea della frattura.
In pratica gli oggetti se sottoposti ad uno stress tendono a rompersi dopo un certo tempo in questo caso si parla di fatica.
La fatica è caratterizzata dal fatto che si presenta nei materiali a contatto con una atmosfera con un certo grado di umidità relativa, non si manifesta a bassa temperatura ed anzi l’aumento di temperatura favorisce la fatica, essa è inoltre indipendente dalle dimensioni della frattura.
2.4.1) Fatica statica
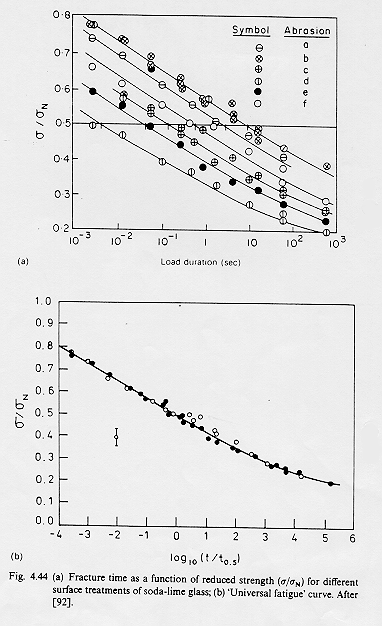
Nella figura 15 § 7.7 si fa l’esempio di un vetro sodio-calcio-silicatico precedentemente abraso in modi diversi e sottoposto ad un carico costante in questo modo si può misurare il tempo di frattura.
Se normalizziamo lo stress misurato alla temperatura sperimentale rispetto alla resistenza s N calcolata alla temperatura dell’azoto liquido ed il tempo di frattura t ad un tempo t0,5 tale che lo stress misurato s sia uguale a metà di s N, si ottiene così la curva universale di fatica.
Figura 15 § 7.7
Fatica dinamica
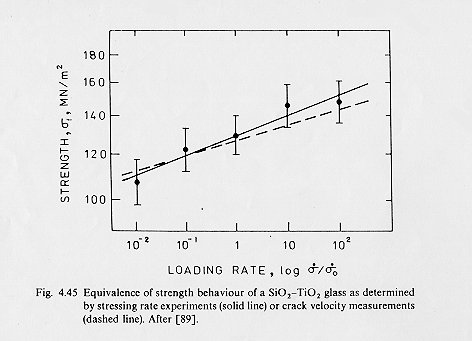
In questo caso il carico sul campione viene aumentato con una velocità costante, viene misurato lo stress al punto di frattura in funzione della velocità di carico ottenendo una retta che in figura 16§ 7.8 viene comparata con quella (tratteggiata) che unisce i valori di s F ottenuti dal modello della velocità di frattura.
Figura 16 § 7.8
Durabilità
Usando la curva universale della fatica statica si ottiene direttamente la durabilità tuttavia la creazione di questa retta è un procedimento lento e tedioso, in genere é sufficiente considerare che ![]() che permette una stima prudenziale di tf a dati stress dopo che si è determinato il minimo tempo di rottura a due valori di stress generalmente più alti del valore massimo di stress utilizzato.
che permette una stima prudenziale di tf a dati stress dopo che si è determinato il minimo tempo di rottura a due valori di stress generalmente più alti del valore massimo di stress utilizzato.
Comportamento viscoelastico
Il vetro tenuto ad una temperatura lontana dalla temperatura di transizione vetrosa Tg si comporta come un solido idealmente elastico, l’intera deformazione è prodotta nel momento dell’applicazione del carico, non varia nel tempo e s'annulla istantaneamente quando la sollecitazione applicata è tolta. Questo tipo di comportamento viene anche chiamato comportamento elastico fino a rottura ed è in genere tipico dei solidi fragili che non manifestano fenomeni di scorrimento (snervamento). Come abbiamo visto, la legge di Hooke stabilisce che c’è una proporzionalità diretta tra la sollecitazione e la deformazione: ![]() .
.
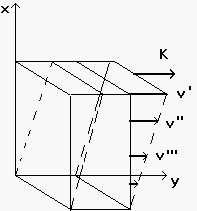
A temperature più alte, superiori alla temperatura di transizione vetrosa Tg, il comportamento del vetro è invece quello di un liquido viscoso ideale o newtoniano. La deformazione viscosa è permanente e la forza di taglio applicata K è proporzionale al gradiente della velocità di deformazione v:
![]()
dove h è la viscosità e ![]() è il gradiente della velocità.
è il gradiente della velocità.
A temperature intermedie il comportamento del vetro non sarà puramente elastico né puramente viscoso bensì avrà delle caratteristiche miste, la risposta a sollecitazioni esterne sarà quindi di natura viscoelastica. In effetti le due risposte non saranno sincrone bensì distinte: al momento iniziale ci sarà una risposta elastica mentre nel tempo una graduale risposta viscosa.
Per spiegare il comportamento viscoelastico del vetro sono stati proposti vari modelli vediamo i principali:
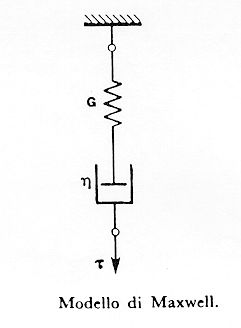
Modello di Maxwell
Come vediamo dalla figura 17, se g è la deformazione tangenziale unitaria tale che ![]() allora
allora ![]()
Figura17
Per spiegare il comportamento viscoelastico dei vetri Maxwell ipotizzò un modello semplificato costituito da una molla e da un ammortizzatore messi in serie (figura 18) § 8.1a; la molla rappresenta il comportamento elastico puro di un solido "hookiano" mentre l’ammortizzatore riproduce il comportamento di un fluido idealmente viscoso ("newtoniano"). L’ammortizzatore è infatti costituito da un pistone con scarsa tenuta che scorre in un cilindro in maniera graduale, il fluido interno al cilindro è costretto, sotto l’azione di una forza, a fluire lateralmente al pistone stesso, quando la forza viene tolta il pistone rimane nella posizione raggiunta.
Figura 18 modello di Maxwell § 8.1a
Se applichiamo una sollecitazione t , a questa saranno soggetti sia l’elemento elastico (molla) che quello viscoso (pistone):
![]()
mentre la deformazione totale g tot è la somma della deformazione elastica e di quella viscosa:
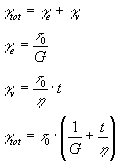
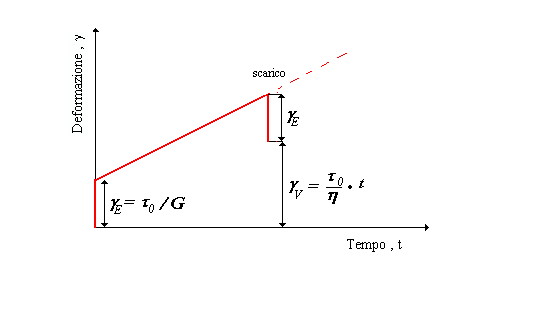
come vediamo nel diagramma di figura 19 § 8.1b il modello prevede una deformazione elastica istantanea seguita da una deformazione viscosa che cresce linearmente nel tempo. Se ad un certo istante si toglie il carico viene recuperata istantaneamente ed integralmente la sola deformazione elastica mentre quella viscosa non è recuperabile.
Figura 19 Deformazione viscoelastica secondo il modello di Maxwell § 8.1b.
Modello di Kelvin-Voigt
In seguito a studi più accurati K-V hanno introdotto accanto alla risposta elastica istantanea un'elasticità differita: una deformazione di tipo elastico che non si manifesta immediatamente all’atto dell'applicazione del carico bensì, è prodotta progressivamente nel tempo a causa di un attrito viscoso che ne ostacola il manifestarsi e ne impedisce il recupero completo in tempi finiti al cessare della forza che ha indotto la deformazione.
Figura 20 modello Kelvin-Voigt § 8.2a
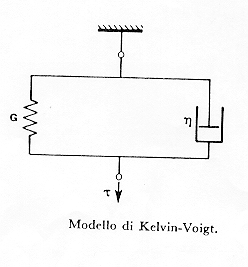
Come vediamo nella figura § 8.2a il modello prevede una molla ed un ammortizzatore messi in parallelo, sotto l’azione di un carico la risposta elastica della molla è ritardata dall’elemento viscoso (il fluido che scorre nel cilindro) in questo caso la deformazione dei due elementi è identica mentre lo sforzo totale viene ripartito tra l’elemento elastico e quello viscoso:
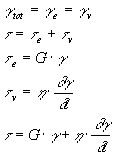
risolvendo per t = t 0 costante si ottiene:
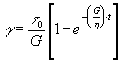
dimensionalmente ![]() è un tempo, esso viene chiamato tempo di ritardo Trit indice del ritardo nella risposta elastica
è un tempo, esso viene chiamato tempo di ritardo Trit indice del ritardo nella risposta elastica
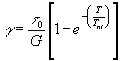
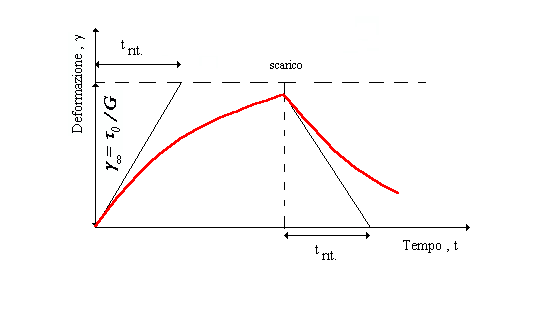
Nel diagramma di figura 21 § 8.2b vediamo che la deformazione massima per ![]() è
è ![]() mentre dopo un tempo t pari al tempo di ritardo la deformazione raggiunge un valore pari a
mentre dopo un tempo t pari al tempo di ritardo la deformazione raggiunge un valore pari a ![]() del valore finale (circa il 63%). Se la sollecitazione viene tolta ad un certo tempo di scarico la deformazione è completamente recuperata in un tempo praticamente infinito.
del valore finale (circa il 63%). Se la sollecitazione viene tolta ad un certo tempo di scarico la deformazione è completamente recuperata in un tempo praticamente infinito.
Figura 21 Deformazione viscoelastica secondo il modello di Kelvin-Voigt § 8.2b
Modello a 4 elementi
Figura 22 modello a quattro elementi § 8.3a
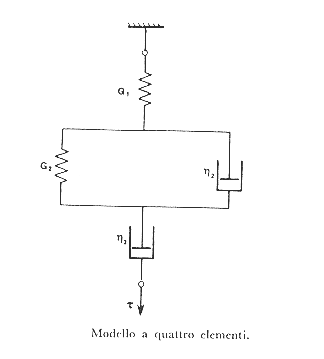
Nel vetro a temperature molto inferiori alla temperatura di transizione vetrosa la deformazione elastica differita non supera il valore del 1-2% della deformazione elastica istantanea quindi in prima approssimazione si può considerare il comportamento di un vetro come quello di un solido puramente elastico, avvicinandosi alla temperatura di transizione vetrosa si ha un aumento nell’entità della risposta elastica differita e quindi per lunghe sollecitazioni si deve tenerne conto, d’altra parte intorno alla temperatura di transizione vetrosa comincia a manifestarsi anche una deformazione puramente viscosa per cui conviene riferirsi ad un modello a 4 elementi § 8.3a in cui una molla è messa in serie ad una ulteriore molla in parallelo con un pistone, a loro volta molla e pistone sono in serie con un pistone finale.
La deformazione totale è data dalla somma di una deformazione elastica pura, di una deformazione elastica differita e di una deformazione viscosa pura:
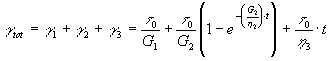
come si vede dalla figura 23 § 8.3b il diagramma della deformazione in funzione del tempo è costituito da una deformazione istantanea dovuta al comportamento "hookiano" del materiale seguita da una deformazione elastica differita (g 2) e quindi da una deformazione viscosa determinata dal comportamento "newtoniano" del vetro, dopo che viene tolta la sollecitazione si ha un recupero immediato della deformazione elastica mentre la deformazione elastica differita viene recuperata in un tempo praticamente infinito, la deformazione viscosa infine non è recuperata affatto.
Figura 23 Analisi delle componenti della deformazione totale, secondo il modello a quattro elementi § 8.3b
Dipendenza del comportamento viscoelastico dalla temperatura
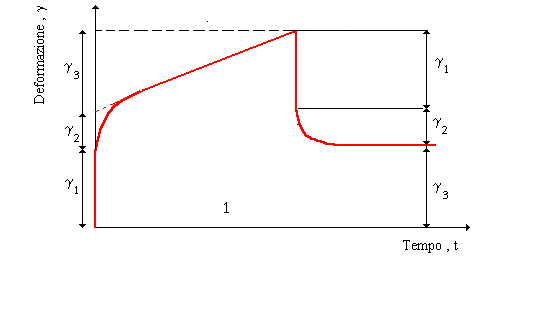
Come vediamo in figura 24 § 8.4 a temperature basse possiamo trascurare i termini relativi alla elasticità ritardata ed alla deformazione puramente viscosa, il comportamento è simile a quello di un solido "idealmente" elastico, avvicinandosi alla temperatura di transizione vetrosa questi due termini diventano sempre più influenti sul comportamento complessivo del materiale mentre a temperature ancora più alte può essere preso in considerazione solo il comportamento "puramente" viscoso
Figura 24 deformazione sotto carico in funzione del tempo a varie temperature§ 8.4
Dipendenza del comportamento viscoelastico dal tempo
Un vetro che ha un comportamento elastico a bassa temperatura può ugualmente presentare un fenomeno di scorrimento viscoso e dar quindi luogo ad una deformazione permanente se la sollecitazione è mantenuta per tempi sufficientemente lunghi, al contrario se si applica ad un vetro ad alta temperatura sollecitazioni per tempi brevissimi si può osservare una risposta di tipo elastico.
tempo di rilassamento: si definisce così il tempo necessario affinché sotto un carico costante la deformazione viscosa raggiunga una entità pari a quella della deformazione elastica istantanea:
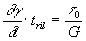
ma poiché
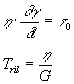
da questa relazione si vede come il comportamento viscoso e/o elastico di un vetro dipende anche dalla entità della sollecitazione in relazione alla sua durata: il comportamento di un vetro si avvicinerà a quello di un fluido viscoso quando la durata della sollecitazione applicata supererà il tempo di rilassamento, al contrario se il tempo di applicazione delle sollecitazione è inferiore al Tril il comportamento del vetro si avvicinerà a quello di un solido elastico.
Ad esempio un vetro da lastra sottoposto ad una sollecitazione pari a t0 = 3000 Kg/mm2 e tenuto ad una temperatura tale che la viscosità h sia di 1014 Poise avrà un tempo di rilassamento di 330 s. per una sollecitazione "immediata" il vetro si comporta in modo elastico. Lo stesso vetro portato alla temperatura di lavorazione (500-600 °C) ha una h = 107 ¸ 108 Poise e quindi il tempo di rilassamento si riduce a Tril = 3 10-4 secondi, in questo caso il vetro si comporta come un fluido viscoso sotto brevi sollecitazioni