Introduzione
Tempo fa lessi un articolo scritto da Raymond Y.Chiao, Paul G. Kwiat e Aephraim M. Steinberg che mi affascinò davvero per le teorie esposte. Per questo ho voluto fornire a tutti questo mio articolo, che riprende alcune delle teorie originali, esposte in maniera più semplice e chiara, anche per i non "addetti ai lavori". Chissà che la lettura di questo testo non vi invogli ad approfondire le vostre conoscenze nell'ambito della fisica quantistica, un campo davvero emozionante.
Superare la luce ?
Tutti noi siamo a conoscenza di uno dei principi basilari della fisica, enunciato da A. Einstein, per il quale nulla si può muovere ad una velocità superiore a quella della luce, ma esiste un fenomeno che sembrerebbe, e dico solo sembrerebbe, mettere in crisi questo enunciato fondamentale. L'effetto in questione è il cosìdetto effetto tunnel, per il quale un particella svanisce di fronte ad un ostacolo per riapparire dall'altra parte dell'ostacolo stesso.
Sono stati eseguiti degli esperimenti nei quali si sono messi, per così dire, a "gareggiare" due fotoni su percorsi di uguale lunghezza, registrando i tempi della "corsa"../../../. La diferenza tra i due percorsi consisteva nel fatto che uno dei due fotoni avrebbe incontrato sul suo cammino una barriera. Si è notato che il comportamento dei due fotoni si accoppiato, benchè nessun segnale possa aver viaggiato da un fotone all'altro, a causa della notevole distanza tra essi. E' necessario fare ora una piccola digressione per poter spiegare in maniera completa il fenomeno.
Se prendiamo in considerazione una qualsiasi palla di dimensioni macroscopiche in movimento, ad essa possiamo assegnare in ogni istante un posizione nello spazio; unendo tutti questi intervalli è possibile quindi ottenere la traiettoria seguita dalla palla stessa, ad ogni punto della suddetta traiettoria è possibile quindi definire la velocità (legata alla sue energia cinetica). Se questa palla viene fatta rotolare su un piano che presenta un dosso, mentre la palla risalirà il dosso, la sua energia cinetica si trasformerà gradualmente in energia potenziale; se la palla non possiede originariamente una sufficiente quantità di energia per attraversare il dosso, essa rotolerà inevitabilmente all'indietro, in fisica questo dosso viene definito come "barriera"../../../.
Quando ci spostiamo invece nel campo della meccanica quantistica, il concetto stesso di traiettoria viene a cadere, in quanto non è più possibile rappresentare la posizione della particella con un semplice punto matematico. La particella viene più correttamente rappresentata mediante un pacchetto d'onda diffuso, che a partire dal bordo posteriore si innalza fino ad un valore massimo per poi decrescere fino al bordo anteriore. La probilità di trovare una qualsiasi particella in una posizione è data dall'altezza massima dell'onda in quell'intervallo, mentre la larghezza del pacchetto d'onda costituisce l'incertezza intrinsecha della posizione della particella. Se però la particella viene rilevata in una data posizione, allora il pacchetto d'onda intero sparisce; in più non possiamo avere informazione riguardo dove si trovava la particella prima di quel momento.
Abbiamo parlato di incertezza nella posizione, questo significa che se una particella è posta di fronte ad un barriera, essa ha una probabilità, seppur piccolissima, di trovarsi dal lato opposto dell'ostacolo, questo prende appunto il nome di "effetto tunnel"../../../. La barriera rimane comunque intatta. Se difatti una particella si trovasse all'interno dell'ostacolo, la sua energia cinetica sarebbe negativa, e siccome la velocità è proporzionale alla radice quadrata del'energia cinetica, non sareremo in grado di estrarre la suddetta radice; quindi non è possibile attribuire una valore di velocità reale alla particella all'interno della barriera.
L'esperimento descritto all'inizio fu eseguito utilizzato una sorgente luminosa in grado di emettere una coppia di elettroni alla volta. La funzione della barriera fu svolta da uno speciale specchio in grado di riflettere fino al 99% della radiazione incidente con energie specifiche. Alla fine di ogni percorso fu posto un rivelatore; nella maggiorparte dei casi quando il fotone incontrò la barriera esso venne respinto indietro, ed in rivelatore fornì una risposta negativa, ma in alcuni giorni di osservazione si notò che oltre un milione di fotoni fu in grado di attraversare l'ostacolo posto sul suo cammino.
La cosa più strana è che, confrontando i tempi di arrivo dei due fotoni quando anche il fotone B attraversava la barriera, si vide che in media arrivavano prima i fotoni che avevano attraversato la barriera stessa! Eseguendo un calcolo sulla velocità del fotone B, si arriva al risultato di una velocità di percorrenza del percorso 1,7 volte superiore a quella della luce.
Per dimostare e spiegare che questo dato è solo apparente ma non corrisponde alla realtà, è possibile riccorrere ad un'altra semplice metafora, vi ripropongo quella esposta nell'articolo originale in quanto, a mio parere, esprime in maniera molto chiara quello che avviene.
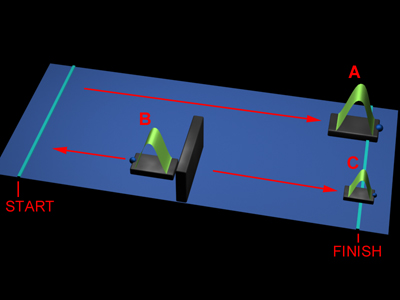
Immaginiamo i due fotoni A e B rappresentati da due tarturughe. La forma del guscio esprime la forma del pacchetto d'onda diffuso esposto prima. Le due tartarughe presentano il naso esattamente sulla linea di partenza, quando viene dato il via le due tarturughe cominciano il loro percorso. Il naso rappresenta una probabilità estremamente piccola di trovare la particella in una posizione. La tarturaga A compie il suo percorso indisturbata, mentre la tartaruga B, quando incontra la barriera, si suddivide in due tartarughe più piccole: una delle due viene riflessa indietro, mentre l'altra attraversa la barriera (la chiameremo tartaruga C ). Queste due tartaruge "parziali" esprimono in effetti la distribuzione di probabilità del fotone singolo.
La tartaruga che viene riflessa ha una dimensione maggiore rispetto alla tarturuga che ha attraversato la barriera perché le probabilità che il fotone venga riflesso sono molto maggiori (quel 99% di riflessione).
Si osservi come i due nasi delle tartarughe A e C siamo sempre allineati, nessuno dei due arriva prima dell'altro, entrambi si muovono alla velocità della luce. Ma la posizione del fotone è meglio espressa dal picco dell'onda (dalla sommità del guscio, probabilità maggiore), quindi benchè i due nasi siano sempre pari pari, il fotone C ha maggiore probabilità di raggiungere l'arrivo prima del fotone A. Si vede difatti che la sommità del guscio C presenta un vantaggio rispetto alla sommità del guscio A.
Non si è quindi ritenuto che una parte del pacchetto d'onda si muova ad una velocità superiore a quella della luce, semmai che avvenga una sorta di ridistribuzione del pacchetto lungo il cammino. Ma per quale motivo avviene il fenomeno della ridistribuzione ? Per spiegare l'effetto tunnel rapido si può partire da un indizio. Secondo la teoria, l'aumento della lunghezza del barriera non comporta un aumento del tempo di attraversamento del pacchetto d'onda. Più breve è il tempo dedicato allo studio di un fotone e minore è la precisione nell'ottenimento di informazioni sulla sua energia; quando un fotone si trova davanti ad una barriera, anche se non ha energia sufficiente per attraversarla, in un certo senso esiste un piccolissimo intervallo di tempo nel quale il suo valore di energia non è definito, in questo intervallo è come se il fotone potesse prendere in prestito una quantità di energia sufficiente per attraversare la barriera; la durata di questo periodo dipenderebbe solo dall'energia presa in prestito, e non dalla lunghezza da attraversare della barriera, il tempo di transito all'interno dell'ostacolo è sempre lo stesso.
(Articolo originale scritto da Raymond Y.Chiao, Paul G. Kwiat ed Aephraim M. Steinber)