La forza di Colioris e' una forza inerziale, cioe' dovuta alla NON-inerzialita' del sistema di riferimento in cui viene osservata (Terra nel caso della legge di Ferrel).
Le forze inerziali sono comunissime: le sperimentiamo su noi stessi ogni volta che andiamo in treno, oppure in automobile. La loro esistenza era stata intuita gia' da Galileo, ma e' Newton, che enuncia: "un corpo in quiete od in moto rettilineo uniforme tende a rimanere nel suo stato di moto o di quiete". Che vuol dire "tende a rimanere"? Per essere chiaro saro' leggermente impreciso: vuol dire che ci sono delle forze, e sono le forze inerziali, che si oppongono al "cambiamento" di velocita' sia come intensita' che come direzione (ed infatti e' quello che sperimentiamo nelle frenate e nelle curve sia in treno che in automobile).
La forza di Coriolis si presenta in un caso un po' piu' complesso: il moto di un corpo che si trova in un sistema di riferimento rotante (per esempio la Terra).
Nel caso di corpo in quiete in un sistema di riferimente rotante, quello che si sperimenta e' solo una forza centrifuga, cioe' una forza che e' diretta come in figura (1).
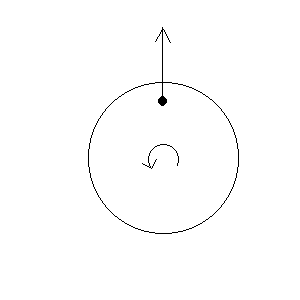
Un esempio di questa situazione (oltre
alle curve durante un viaggio) e' una di quelle vecchie
giostre in cui ci sono dei seggiolini che si "alzano"
man mano che la velocita' aumenta. Questo avviene perche'
i seggiolini (il punto nero nella figura), tenderebbero
ad andare in linea retta, cioe' a girare a destra
rispetto alla direzione del moto imposta dalle funi, che
e' verso sinistra. Per questo appare la forza
"centrifuga", cioe' diretta come in figura.
Nel caso invece di corpo in moto in un sistema di
riferimento rotante la cosa e' analoga, solo che il corpo
"tende a conservare" la velocita' dovuta al suo
moto, oltre a quella impressagli dalla rotazione; in piu'
cosa fondamentale, la velocita' impressagli dalla
rotazione varia mentre il corpo si sposta.
Immaginiamo (figura 2) sempre una vecchia giostra, ma
questa volta di quelle con una piattaforma su cui ci sono
vari cavalli a diversa distanza dal centro. I cavalli
vicino al centro di rotazione sono quasi fermi, mentre
quelli piu' lontani hanno velocita' lineare maggiore.
Questo perche' tutti hanno la stessa velocita' angolare (cioe'
fanno gli stessi giri nello stesso
tempo) ma hanno velocita' lineari diverse, poiche' un
giro vicino al centro avviene in poco spazio, mentre al
bordo possono esserci parecchi metri.
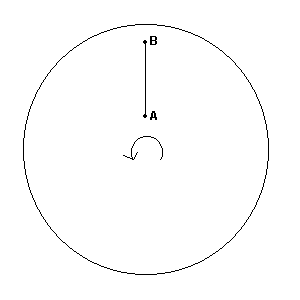
Supponiamo di voler andare lentamente dal punto B al
punto A (rischiando di cadere). Durante il tragitto,
mentre mi sposto da B verso A, la mia velocita' lineare (che
e' verso sinistra) deve diminuire; allora sento una forza
verso sinistra, come quando, in auto, frenando la mia
velocita' (che e' in avanti) sento una forza che mi
spinge in avanti. Questa forza "verso sinistra"
si somma ovviamente a quella centrifuga e rende difficile
camminare su queste giostre.
Supponiamo adesso di voler tornare lentamente dal punto A
al punto B. In questo caso la mia velocita' lineare deve
aumentare, cioe' devo accelerare verso sinistra; allora
sento una forza verso destra (come quando in accelero
automobile e sento una forza che mi spinge indietro,
"tendo a restare indietro" rispetto alla
direzione della velocita'). In questo caso e' facile
pensare a questa forza come dovuta al fatto che la
giostra ruota sotto i miei piedi e pertando, se vado in
linea retta, in realta' mi trovero' spostato piu' a
destra.
Le considerazioni qualitative svolte nel caso delle
giostre valgono ovviamente per qualsiasi sistema di
riferimento rotante, compresa la Terra.
Quantitativamente la forza di Coriolis ha un'espressione
che fa uso del prodotto vettoriale, poiche' l'effetto e'
dovuto alla velocita' perpendicolare all'asse di
rotazione (in effetti non c'e' nessuna forza
inerziale nel su e giu' dei cavalli, che e' una velocita'
parallela all'asse di rotazione).
Ritornando alla legge di Ferrel, prendiamo un globo
terrestre, senza il quale sara' un po' complesso seguire
questo ragionamento. Ponendo il globo in rotazione in
senso antiorario (visto dal polo Nord), e' intuitivo che
una corrente d'aria che si diriga verso l'equatore resti
"indietro", poiche' all'equatore la velocita'
lineare e' massima, mentre vicino ai poli questa velocita'
era minima. Nell'emisfero Nord (in cui devo andare a Sud,
per raggiungere l'equatore) avro' una deviazione verso
destra, mentre nell'emisfero Sud (in cui l'equatore e'
piu' a Nord) avro' una deviazione verso sinistra.
Al contrario una corrente che proviene dall'equatore avra'
una velocita' lineare maggiore di quella che dovrebbe
avere vicino ai poli per seguire la rotazione terrestre,
e percio' "girera' piu' veloce della Terra",
cioe' deviera' a destra andando verso Nord, a sinistra
andando a Sud.