Le risorse idriche

Criteri speditivi di calcolo delle zone di rispetto
per pozzi ad uso potabile

L’instaurarsi di un pompaggio in falda comporta una modifica locale dell’assetto idrodinamico dell’acquifero. In condizioni di riferimento (a pozzo fermo) il moto dell’acqua nella falda avviene secondo il naturale gradiente idraulico J e le linee di flusso e quelle equipotenziali (che rappresentano rispettivamente la direzione del moto e il carico piezometrico) in condizioni di moto laminare in un mezzo omogeneo e isotropo sono due insiemi di rette parallele che si intersecano ortogonalmente.

Il pompaggio, d’altro canto, considerato a sé stante, genera una serie di curve equipotenziali corrispondenti a cerchi con centro nel pozzo idrico e linee di flusso identificate con raggi che hanno origine anch’essi dal pozzo.

La combinazione di questi due sistemi di flusso in seno all’acquifero dà luogo alle effettive condizioni del moto in una falda dotata di gradiente idraulico J e soggetta a pompaggio. Si viene quindi a determinare una “zona di influenza” del pozzo cioè un’area dove l’acqua contenuta nello strato saturo del terreno viene via via richiamata verso il pozzo stesso.

E’ evidente come, all’interno di questa zona, un inquinante venga trascinato verso il pozzo, e quindi possa avvenire la contaminazione della risorsa idrica.E’ possibile, utilizzando la teoria del pompaggio da pozzo in condizioni stazionarie, tracciare il profilo della piezometrica lungo una sezione verticale che passi per il pozzo. Intuitivamente, almeno in prima approssimazione, si può tentare di individuare questa “zona di influenza” e assumerla come ZR ristretta, ai sensi dell’art. 21 del D. L.vo 152/99.

Per studiare il fenomeno in termini analitici occorre essere in possesso dei parametri che caratterizzano il moto nell’acquifero. In particolare bisogna conoscere la portata emunta dal pozzo (Q), la quota del tetto della falda in condizioni di flusso indisturbato nel punto ove insiste il pozzo (H), il raggio del pozzo (r), la trasmissività dell’acquifero (T) e il gradiente idraulico naturale della falda (J). Inoltre devono essere soddisfatte alcune condizioni che consentono di approssimare il problema analitico, consentendone una soluzione relativamente semplice:

(metodo della ricarica)

(metodo volumetrico)

Se t/t* < 0,1 il raggio d’azione si calcola come un cerchio con centro il pozzo e raggio pari a:

se 0,1 < t/t* <= 1 allora si ha:

Stavolta il cerchio non sarà centrato sull’asse del pozzo, ma presenterà un’eccentricità ? rivolta contro il senso del flusso naturale della falda, il cui valore è:

Si ottiene una retta, il cui cambio di pendenza indica il valore della portata critica.

Criteri speditivi di calcolo delle zone di rispetto per pozzi ad uso potabile
PREMESSA I criteri per la tutela delle risorse idriche destinate al consumo umano vengono, dal punto di vista normativo, illustrati nell’art. 21 del D.L.vo 152/99, e in questa sede non si indulgerà nel citare quanto prescrive la ben nota norma richiamata. L’aspetto che si intende approfondire in queste note è la determinazione della zona di rispetto per i pozzi idrici, al di là della prescrizione, per la verità puramente orientativa, di assumerne l’estensione pari alla circonferenza con centro il pozzo e raggio uguale a 200 m. Tale indicazione viene suggerita laddove la Regione non abbia già provveduto alla identificazione delle aree di rispetto, secondo quanto indicato al comma 1) dell’art. 21 stesso. Sembra opportuno tentare di affrontare e approfondire tecnicamente questa problematica in quanto, a seconda dei casi in studio, il criterio fisso geometrico può risultare o eccessivamente cautelativo o addirittura non adeguato a proteggere effettivamente la risorsa idrica. Questo lavoro non può assolutamente impegnarsi nella vastissima tematica che è stata ed è tuttora scientificamente elaborata da eminenti studiosi nel campo dell’idraulica dei pozzi. Si cercherà soltanto di fornire qualche indicazione semplice, con approssimazioni nell’assunzione delle ipotesi di lavoro che, nella maggioranza dei casi, possono essere accettate a fronte del risultato ottenuto. Ci si pone, inoltre, nell’ipotesi di piccole derivazioni, in cui esista una limitata disponibilità di risorse tecnico-economiche, tali da non consentire una completa campagna di indagini in pieno campo per la determinazione in maniera esaustiva di tutti i parametri necessari alla caratterizzazione del flusso idrico nell’acquifero.

INQUADRAMENTO DEL PROBLEMA Il Decreto 152/99, come già il D.P.R. 236/88, pone delle limitazioni negli usi del territorio all’interno delle aree di salvaguardia della risorsa idrica: Zona di Tutela Assoluta (ZTA) Zona di Rispetto (ZR) e Zona di Protezione (ZP). Viene introdotto il concetto di Z.R. ristretta e Z.R. allargata, secondo una filosofia che porterebbe nel tempo la ZR ristretta a coincidere con la ZR allargata. E’ stabilito che la captazione di una risorsa idrica per il consumo umano istituisce, attraverso l’individuazione delle zone di protezione, un vincolo sicuramente pesante per il futuro sviluppo di attività antropiche nella zona, sia che si parli di insediamenti abitativi che industriali o agricoli. Per le attività o insediamenti esistenti occorre, ove possibile, procedere al loro allontanamento al di fuori della ZR, e comunque deve essere assicurata la messa in sicurezza dei centri di pericolo. E’ sicuramente chiaro a tutti quindi che la determinazione della zona vincolata è un passaggio delicato, per le implicazioni che ne derivano a carico della collettività, a fronte dell’esigenza imprescindibile di tutelare la salute degli utenti della risorsa idrica e anche, non dimentichiamolo, salvaguardare l’equilibrio idrogeologico quali-quantitativo dell’area d’intervento. Il criterio generale che identifica in un cerchio di raggio 200 m la ZR non risponda sempre in maniera convincente alle effettive esigenze tecniche derivanti dallo studio del territorio, con le sue caratteristiche morfologiche e la sua struttura idrogeologica e con diversificate attività antropiche inevitabilmente esistenti al momento dell’intervento. Occorre quindi individuare in maniera rigorosa, anche al di fuori della ZR di legge, i possibili centri di pericolo, identificare poi la ZR con le metodologie più avanti sintetizzate e quindi trarre le relative conclusioni, fissando alcune soglie di rischio accettabile per la problematica esaminata.

LA ZONA D’INFLUENZA DEL POZZO
L’instaurarsi di un pompaggio in falda comporta una modifica locale dell’assetto idrodinamico dell’acquifero. In condizioni di riferimento (a pozzo fermo) il moto dell’acqua nella falda avviene secondo il naturale gradiente idraulico J e le linee di flusso e quelle equipotenziali (che rappresentano rispettivamente la direzione del moto e il carico piezometrico) in condizioni di moto laminare in un mezzo omogeneo e isotropo sono due insiemi di rette parallele che si intersecano ortogonalmente.
Il pompaggio, d’altro canto, considerato a sé stante, genera una serie di curve equipotenziali corrispondenti a cerchi con centro nel pozzo idrico e linee di flusso identificate con raggi che hanno origine anch’essi dal pozzo.
La combinazione di questi due sistemi di flusso in seno all’acquifero dà luogo alle effettive condizioni del moto in una falda dotata di gradiente idraulico J e soggetta a pompaggio. Si viene quindi a determinare una “zona di influenza” del pozzo cioè un’area dove l’acqua contenuta nello strato saturo del terreno viene via via richiamata verso il pozzo stesso.
E’ evidente come, all’interno di questa zona, un inquinante venga trascinato verso il pozzo, e quindi possa avvenire la contaminazione della risorsa idrica.E’ possibile, utilizzando la teoria del pompaggio da pozzo in condizioni stazionarie, tracciare il profilo della piezometrica lungo una sezione verticale che passi per il pozzo. Intuitivamente, almeno in prima approssimazione, si può tentare di individuare questa “zona di influenza” e assumerla come ZR ristretta, ai sensi dell’art. 21 del D. L.vo 152/99. Per studiare il fenomeno in termini analitici occorre essere in possesso dei parametri che caratterizzano il moto nell’acquifero. In particolare bisogna conoscere la portata emunta dal pozzo (Q), la quota del tetto della falda in condizioni di flusso indisturbato nel punto ove insiste il pozzo (H), il raggio del pozzo (r), la trasmissività dell’acquifero (T) e il gradiente idraulico naturale della falda (J). Inoltre devono essere soddisfatte alcune condizioni che consentono di approssimare il problema analitico, consentendone una soluzione relativamente semplice:
la conducibilità idraulica entro il cono di depressione è uniforme il terreno non è stratificato, cioè la conducibilità orizzontale è uguale a quella verticale lo spessore della falda è costante il pozzo ha un'efficienza idraulica del 100% il pozzo è completo, cioè filtra tutta la falda la superficie d'acqua è orizzontale prima del pompaggio il flusso è laminare il cono di depressione ha raggiunto lo stato di equilibrio
Consideriamo per semplicità il pompaggio di un pozzo in un acquifero confinato. In questo caso, in condizioni permanenti, l’equazione che regola gli abbassamenti del livello piezometrico è:
	Q portata del pozzo T trasmissività H pressione idrostatica h altezza d'acqua nel pozzo R raggio d'influenza del pozzo r raggio del pozzo	Dalla formula si può ricavare la depressione della piezometria nell'intorno del raggio di influenza del pozzo o in altre parole gli abbassamenti della piezometrica lungo una sezione del pozzo secondo le linee di flusso.
Volendo affinare la formula, bisogna considerare la sovrapposizione dell’effetto del pompaggio sul moto dettato dal gradiente naturale di falda, quindi si ha:
	La relazione individua, per il punto a distanza x dall’asse del pozzo, il valore della quota piezometrica z, somma dell’altezza dinamica nel pozzo (h) più l’aliquota di carico dovuto al pompaggio (Dh), più l’ulteriore aliquota di carico dovuto al gradiente naturale del moto indisturbato (Dh0).
Assegnando quindi una serie di valori alla distanza x, si ottengono i corrispondenti abbassamenti della linea piezometrica lungo una sezione verticale passante per l’asse del pozzo di pompaggio tracciata secondo la direzione del flusso.

Questa procedura, in condizioni di regime, consente di ricostruire il livello piezometrico lungo l’asse di flusso passante per il pozzo. A monte di esso, la piezometrica tende a raggiungere il valore indisturbato (H) mentre a valle si avrà un recupero e, superato un punto in cui la tangente alla piezometrica sarà orizzontale (flusso nullo) la stessa tenderà al valore di moto indisturbato. Per i nostri scopi è importante stabilire:
1. la distanza dal pozzo in cui l’effetto del pompaggio è trascurabile (R raggio d’influenza del pozzo) 2. la distanza a valle del pozzo in cui si verifica la condizione di flusso nullo (Xs, punto di stagnazione) 3. la larghezza della zona, misurata trasversalmente all’asse del flusso, ove si verifica il fenomeno di richiamo di acqua della falda verso il pozzo (F, fronte di richiamo del pozzo).
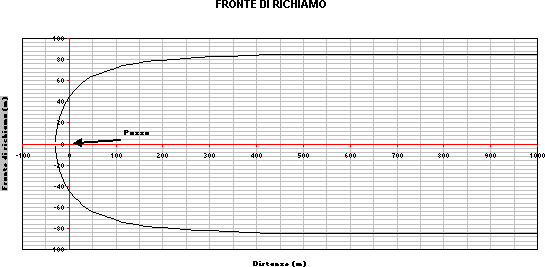
Tutte queste informazioni concorrono ad identificare sul territorio la zona di influenza del pozzo. Per costruire la curva che rappresenta il fronte di richiamo occorre preliminarmente conoscere alcuni tra i già citati parametri fondamentali, quali portata Q, trasmissività T e gradiente idraulico J. Le relazioni fondamentali sono:
	Punto di stagnazione
	Fronte di richiamo
	Equazione dello spartiacque
A questo punto assegnando via via i valori di y (simmetrici rispetto all’asse di flusso), si ricavano con l’equazione dello spartiacque le corrispondenti distanze dal pozzo ove il fronte di richiamo ha larghezza 2y.

Evidentemente, il problema è calcolare la distanza limite R, per definire una zona di rispetto ristretta della risorsa. L’approccio analitico a questo punto fa ricorso a modelli matematici di simulazione di flusso in falda, dei quali daremo oltre qualche semplice cenno. Sempre invece in termini speditivi, si possono citare due metodi approssimati e che comunque necessitano di valutazioni soggettive dell’operatore in merito alla situazione particolare che si esamina. 1. Metodo della ricarica (recharge method) 2. Metodo volumetrico (volumetric method) Entrambi i metodi fanno riferimento a una specifica relazione che esprime un bilancio idrico:
	N è la piovosità (m/d) Q è la portata (m3/d) H è lo spessore dell’acquifero saturo (m) R è il raggio della superficie cilindrica (m) t è il tempo di osservazione del bilancio (d) n è la porosità dell’acquifero
Ne deriva che:
Quando t è molto grande si ha un raggio d’influenza che rappresenta la zona di cattura completa, e la relazione diventa:		(metodo della ricarica)
Quando invece t è breve, ovvero sono scarse le precipitazioni N si ha:		(metodo volumetrico)
Ambedue le procedure conducono comunque a una zona d’influenza circolare, dove bisogna fissare dei parametri (ad esempio t) in quanto con il metodo della ricarica si ottengono in genere aree molto estese, soprattutto nelle aree di scarsa piovosità come la Sicilia.

Un altro metodo approssimato, applicabile in casi semplici, con acquiferi poco complessi, assumendo un tempo di funzionamento t ragionevolmente elevato e comunque adottando larghi margini di sicurezza, si basa sulla definizione di un parametro adimensionale definito dal rapporto t/t* dove:
		Q0 portata specifica dell’acquifero H spessore dell’acquifero n porosità del mezzo Q portata del pozzo
Se t/t* < 0,1 il raggio d’azione si calcola come un cerchio con centro il pozzo e raggio pari a:
se 0,1 < t/t* <= 1 allora si ha:
Stavolta il cerchio non sarà centrato sull’asse del pozzo, ma presenterà un’eccentricità ? rivolta contro il senso del flusso naturale della falda, il cui valore è:
xs è la distanza tra il pozzo e il punto di stagnazione, di cui si è fatto cenno prima. Infine, quando t/t* > 1 allora si procede praticamente alla costruzione della curva spartiacque tramite l’equazione vista prima:

assumendo come limite verso monte (cioè in direzione contraria al flusso naturale rispetto al pozzo) il valore:
Si ricorre a queste procedure semplificate quando, come già detto, non si dispone di sufficienti informazioni sulla struttura e sulla dinamica dell’acquifero tali da implementare un modello di calcolo che tenga conto in maniera quanto più rigorosa possibile di tutti i fattori reali che influenzano il fenomeno di moto (limiti dell’acquifero, disomogeneità dello stesso in relazione a variabilità di spessore e/o di conducibilità idraulica etc.). E’ chiaro che l’influenza dei vari elementi sarà valutata dal tecnico in funzione della scala del problema, e si potrà di volta in volta optare per un’analisi semplificata o più rigorosa. Un approccio corretto è quindi quello di correlare il criterio geometrico di delimitazione della zona d’influenza con il criterio temporale, che si traduce nello stabilire i tempi di deflusso per gli ipotetici inquinanti, in modo da potere, con ragionevole anticipo, individuare la contaminazione e provvedere al risanamento e alla messa in sicurezza del centro di pericolo prima che il contaminante abbia raggiunto il punto di emungimento.

UTILIZZO DELLE PROVE DI POMPAGGIO PER DETERMINARE LA ZONA D’INFLUENZA
Nell’ipotesi dello studio di una risorsa (pozzo) situata in un’area che non sia possibile caratterizzare in dettaglio dal punto di vista idrogeologico, vediamo come si può con una certa approssimazione definire alcune caratteristiche del sistema pozzo in pompaggio – falda, allo scopo di individuare la zona d’influenza del pozzo stesso. Tale studio quindi può condursi a partire dalle prove di pompaggio. A tale scopo si distinguono: * Prove in regime transitorio (a portata costante) test dell’acquifero * Prove in regime di equilibrio (a gradini di portata) test del pozzo o La prova in regime di non-equilibrio (lunga durata). Si tratta di una prova a portata costante protratta per 36-72 ore (valori maggiori per acquiferi non confinati). Si misurano i valori degli abbassamenti in funzione del tempo trascorso presso uno o più piezometri posti a distanza nota dal pozzo. Questo tipo di prova è finalizzata alla determinazione della tipologia idraulica dell’acquifero e dei parametri che caratterizzano il comportamento idrodinamico del sistema messo in pompaggio. Gli inconvenienti del metodo sono dovuti alla necessità di scavare almeno un altro pozzo di osservazione e di dover protrarre a lungo il pompaggio per esplorare l’evoluzione del processo. Facendo riferimento all’espressione semplificata di Jacob per il calcolo degli abbassamenti in regime transitorio per acquifero confinato si ha:
	s è l’abbassamento in punto di osservazione distante x dal pozzo T è la trasmissività S è il coefficiente d’immagazzinamento t è il tempo di pompaggio Q è la portata del pozzo (costante)
Utilizzando il procedimento di Jacob (di tipo misto analitico-grafico), si costruisce il grafico abbassamenti (s) – tempo (t) in coordinate semi-logaritmiche, e da esso si ottengono i valori di T ed S.

E’ possibile approfondire ulteriormente i risultati della prova, ottenendo ulteriori informazioni utili alla caratterizzazione della zona di influenza del pozzo. Supponiamo di analizzare i dati relativi a un certo tempo t della prova di pompaggio: t = 3600 secondi in corrispondenza s = 14,17 m al piezometro posto a x = 110 m dal pozzo. Si costruisce la curva abbassamenti – log (distanza) a parametro t.

L’intercetta della retta così ottenuta sull’asse delle ascisse (distanze) rappresenta la distanza alla quale l’abbassamento risulta nullo e quindi è il valore del raggio di azione del pozzo R per quel dato tempo di pompaggio. Cambiando valori di t si ottengono rette parallele a quella della figura e in corrispondenza diversi valori di R. Si assumerà il valore che corrisponde ai criteri temporali prescelti per la specifica situazione di vulnerabilità. Tali risultati ricavati dalla costruzione grafica si possono pure ottenere eguagliando a zero l’espressione di Jacob (s = 0, quindi x = R):

A titolo esemplificativo, con i dati utilizzati per la costruzione dei grafici di cui sopra si è ottenuto:
	t (ore) R (m) 1 367 9 1100 72 3100
La forma della curva s – t dà una idea qualitativa della natura dell’acquifero investigato. E’ da rilevare che, nel caso di acquifero non confinato, il procedimento di Jacob di può estendere alla determinazione della porosità efficace ne che gioca lo stesso ruolo del coeff. di immagazzinamento S nella espressione che fornisce il valore dell’abbassamento s.
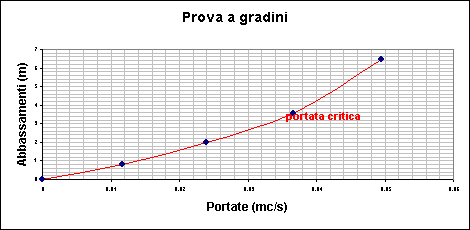
o La prova a gradini (regime permanente) In questo caso si esegue la prova con portate diverse, ma costanti per ogni periodo, aumentando via via il pompaggio. I periodi sono dell’ordine di qualche ora, e si misura per ogni gradino, l’abbassamento stabilizzato nel pozzo. Non è necessario quindi disporre di altri punti di osservazione. Questo tipo di prova serve a caratterizzare la capacità del pozzo, stabilendo la portata ottimale, immediatamente inferiore a quella critica. Non ci fornisce invece gli elementi caratteristici dell’acquifero (T, S, ne) determinabili invece con la prova a portata costante e lunga durata. Si riportano quindi i valori degli abbassamenti s0 del livello nel pozzo in funzione del valore della portata, secondo la relazione:

Si ottiene una retta, il cui cambio di pendenza indica il valore della portata critica.

D’altro canto la relazione di cui sopra è valida anche per tutti i punti del campo del moto radial-simmetrico verso il pozzo, per cui si può scrivere:

Allora si traccia in coordinate semilogaritmiche (s – logx) la retta che passa per il punto P* e che ha coeff. angolare uguale a 0,366*Q/T. Il punto in cui la stessa interseca l’asse delle distanze x corrisponde al valore di R, distanza alla quale l’abbassamento è nullo.

Tale procedimento, analogamente a quanto visto nella prova a portata costante, può essere ripetuto con gli altri gradini di portata, ricavando diversi valori di R. Si vede ancora una volta che, nella definizione di R, anche nei procedimenti semplificati è necessario fissare un orizzonte temporale da mettere in relazione con l’ampiezza della zona di rispetto. Nel seguito si darà un brevissimo cenno a procedimenti più complessi che individuano la zona d’influenza del pozzo cercando di tenere in debita considerazione le caratteristiche reali dell’acquifero, prima fra tutte la presenza di un moto proprio in falda.

I MODELLI DI FLUSSO IN FALDA
Attraverso una ricerca su Internet si è reperito un significativo, sebbene conciso, elenco di software per la modellazione (metodo degli elementi analitici) del comportamento idrodinamico di acquiferi ove ha sede un’attività di estrazione di acqua attraverso un pozzo, al fine di definire in termini più rigorosi la zona d’influenza del pozzo stesso. WhAEM2000 (Wellhead Analytic Element Model) L’agenzia statunitense per la protezione dell’ambiente (U.S. EPA) ha sviluppato un software gratuito per lo studio idrogeologico del sottosuolo. Il programma è indirizzato all’individuazione interattiva della zona di influenza del pompaggio con metodi semplici (criterio del raggio fisso) o più complessi (pozzo in moto di falda uniforme). E’ possibile impostare il calcolo sulla base di mappe georeferenziate o anche semplici mappe acquisite tramite scansione ed esportate in formato autocad dxf. La modellazione idrogeologica in condizioni di regime di pompaggio in falda tiene conto di limiti idrogeologici (fiumi, zone di ricarica) discontinuità geologiche, disomogeneità locali di trasmissività, etc.. Più avanti si fornirà un semplice esempio di calcolo. Per maggiori informazioni sul softwtware: http://www.epa.gov/ceampubl/gwater/whaem/index.htm. Si consiglia l’utilizzo dell’ultima versione (v 2.0.3 Beta). Ottimo il manuale in formato pdf. VisualBlueBird Si tratta di un altro modello dotato, come WhAEM2000, di una gradevole interfaccia grafica per Windows. Funziona su un algoritmo di calcolo chiamato Split, che effettua una modellazione analitica di flusso in un acquifero eterogeneo ma non multifalda. Presenta funzionalità analoghe a WhAEM2000, ma la gestione delle mappe è meno agevole E’ un po’ più semplice nell’interfaccia, ma non dispone di manuale ed esempi validi come WhAEM2000. L’indirizzo per eventuale download (il software è gratuito) è: http://www.groundwater.buffalo.edu/software/VBBandSplit.exe Whpa E’ in pratica una raccolta di modelli di simulazione dell’interazione falda - pozzo con un’interfaccia DOS piuttosto spartana ma efficace. E’ anche questo un software di produzione U.S. EPA. Particolarmente interessante e corposo (in pratica un vero trattato!) il manuale in formato pdf). E’ reperibile all’indirizzo: http://www.epa.gov/ada/download/models/whpa.pdf 3DFlow Suggestivo software di modellazione tridimensionale dell’acquifero con pompaggio, ricco di opzioni ma piuttosto ostico nell’interfaccia DOS. Può studiare pozzi incompleti e acquiferi con varie configurazioni. Da provare. E’ disponibile un manuale piuttosto stringato con un piccolo esempio. Indirizzo: http://groundwater.ce.ksu.edu/3DFlow.zip Infine, si riportano alcuni indirizzi internet che trattano della modellazione del moto negli acquiferi: http://www.engr.uga.edu/~mbakker/srk_cmwr2002.pdf http://water.usgs.gov/pubs/twri/twri-3_B8/pdf/twri_3b8.pdf ftp://slate.mines.edu/pub/wwingle/uncert/manual/UNCERT_manual.pdf http://www.epa.gov/ada/download/project/wellhd.pdf http://www.epa.gov/athens/software/whaem/press.pdf

ESEMPIO DI APPLICAZIONE DEL MODELLO WhAEM2000
La fase preliminare ha inizio con la definizione di un nuovo progetto. Quindi è possibile caricare le mappe tematiche (rete viaria, rete idrografica, insediamenti antropici etc.) che si sovrappongono analogamente ai layer di un programma di grafica vettoriale. Tali mappe sono files con estensione bbm (Binary Base Map). In alternativa, come nell’esempio in parola, si può convertire un file in formato dxf in file bbm e adottarlo come mappa. Si è quindi utilizzato uno stralcio di mappa 1:5000, derivato da un ingrandimento di una carta 1:10000.

A questo punto, visualizzato il territorio ove si opera, ha inizio la fase di input vera e propria. Per iniziare si è posizionato un pozzo di emungimento con le seguenti caratteristiche:
Q = 860 m3/d = 10 l/s portata del pozzo r0 = 0,2 m raggio del pozzo R’ = 200 m raggio della zona di rispetto (come da normativa)
Poi si sono assegnate alcune caratteristiche dell’acquifero, necessarie per il funzionamento del processo di calcolo.
Z0 = 50 m quota della base dell’acquifero H = 30 m spessore dell’acquifero K = 70 m/d permeabilità n = 0,2 porosità
Va definito di seguito un punto dove sono note le caratteristiche del moto naturale della falda (carico piezometrico, direzione, verso e gradiente idraulico del flusso). Nel caso in studio si ha:
Hp = 80 m carico piezometrico nel punto P alfa = 180° direzione da destra a sinistra in orizzontale j = 0,001 gradiente idraulico naturale
E’ possibile inserire numerosi altri “elementi analitici” come fiumi, laghi, aree di disomogeneità (ricariche da apporti meteorici, variazioni locali di permeabilità, contatti geologici con brusca caduta di trasmissività etc.). Per non appesantire eccessivamente queste note, non si è fatto ricorso a queste ulteriori opzioni, che comunque sono ampiamente discusse nell’esempio di calcolo riportato sull’eccellente manuale del programma. Terminata la fase di input, si avvia la risoluzione del modello, attivando la visualizzazione del tracciato delle particelle richiamate dal pozzo e le isopiezometriche. E’ possibile evidenziare le isocrone nel cono di influenza relative a diversi intervalli di tempo. Nel caso trattato si sono scelte le isocrone a 1, 2 e 3 anni. Il risultato è visualizzato nel grafico seguente, dove è indicata per confronto la zona di rispetto “di norma”, cioè un cerchio di raggio 200 m con centro nell’asse del pozzo.

Si possono sperimentare con relativa semplicità gli effetti causati dalle variazioni dei vari elementi che caratterizzano l’input del modello, in quanto i tempi di calcolo sono davvero rapidi. Una notazione, per finire: il software non funziona a dovere (il calcolo si blocca visualizzando un messaggio d’errore o non visualizza i risultati) se non si impostano le unità statunitensi nel Pannello di Controllo > Impostazioni internazionali di Windows.

CONCLUSIONI
Dal lavoro sin qui sviluppato emerge la necessità di caratterizzare maggiormente, dal punto di vista tecnico, l’approccio per la definizione della zona di rispetto delle risorse idro-potabili. Dai risultati della simulazione matematica tramite un modello di calcolo si vede come, a seconda dei casi, il criterio del raggio fisso, non tenendo conto delle reali condizioni di flusso in falda, può non essere cautelativo. Occorre quindi sviluppare dei criteri di definizione della ZR tanto più rigorosi quanto maggiore è la disponibilità di informazioni sulle caratteristiche idro-geologiche dell’acquifero, partendo dai dati ricavabili dalle prove di portata e incrociando il procedimento che porta all’individuazione di R con il calcolo del fronte di richiamo F, verificando ancora i dati con i metodi semplificati (metodo della ricarica, metodo volumetrico e metodo del rapporto t/t*). Se poi esiste una base dati dell’acquifero soddisfacente, si potrà tentare di applicare un modello di flusso secondo il “metodo degli elementi analitici”.

E' disponibile la versione in formato PDF di questo studio:		Cliccare
Bibliografia Oltre ai riferimenti Internet citati si sono consultati i sotto elencati lavori:

1. Castany G. 2. CHIESA G. 3. CHIESA G. 4. CHIESA G. 5. HAMILL L. BELL F.G. 6. IPPOLITO F. e altri	Idogeologia - principi e metodi Idraulica delle acque di falda Pozzi per acqua Inquinamento delle acque sotterranee Acque sotterranee - ricerca e sfruttamento Geologia tecnica	Libreria Dario Flaccovio Editore Dario Flaccovio Editore Ed. HOEPLI Ed. HOEPLI Dario Flaccovio Editore ISEDI Pertini Editore

Nota:	Per chi volesse approfondire gli sviluppi matematici:	Well