CONDIZIONI AL CONTORNO

Nello studio della propagazione del campo elettromagnetico,è essenziale definire delle condizioni al contorno o di continuità,allo scopo di ricavare le soluzioni del problema applicando le equazioni di Maxwell in forma differenziale, come è noto infatti dai corsi di Analisi,affinché un problema risolvibile tramite delle equazioni differenziali abbia soluzione unica è necessario assegnare delle condizioni al contorno sulla funzione da ricavare,mentre le condizioni di continuità sono indispensabili per unire fra loro soluzioni delle equazioni di Maxwell relativa a due diversi materiali,in corrispondenza della superficie di interfaccia.

Risolvendo le equazioni di Maxwell nella forma integrale, attraverso delle ipotesi e considerazioni importanti, si giunge alla determinazione delle condizioni al contorno per dielettrici e per conduttori,

Condizioni al contorno caso due Dielettrici :

Considero le forme integrali                  ∫ E · dl = - ∂ ρ\ ∂ t ∫∫ B · dS        

                                                            ∫ H · dl = ∫∫ J · dS + ∂ ρ\ ∂ t ∫∫ D · dS   

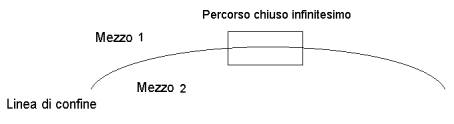
Ipotizzo :    dati due mezzi Dielettrici (1) e (2) a contatto tra di loro,demarcando la linea di confine distinguiamo i due mezzi, ora nell’interfaccia tra questi due mezzi Dielettrici delimitiamo un percorso chiuso racchiudendo un area infinitesima, in queste condizioni applichiamo le  equazioni di Maxwell a quel contorno, piu’ precisamente l’integrale di linea ed otteniamo :

Et1 = Et2                In forma vettoriale : n x (Et1 – Et2 ) = 0

  Ht1= Ht2                   In forma vettoriale : n x (Ht1 – Ht2 ) = 0

Le componenti Tangenziali del campo E e H non cambiano nel passaggio da un mezzo ad un altro.

Considero la forma integrale           ∫∫ D · dS  =  ∫∫ ε E · dS = Q            ∫∫ B · dS  = 0

Ipotizzo :     Facendo le stesse ipotesi di prima,  ora però invece di un percorso chiuso tra le due superfici, si considera una piccola area infinitesima su ciascun mezzo sia A che B in prossimità della linea di confine, si ipotizza poi una densità di carica (ρ) presente sull’interfaccia,applicando quindi l’equazione su questo volumetto elementare si ottiene :

Dn1 - Dn2 =  ρ              Bn1 = Bn2

Nel caso in cui non siano presenti cariche libere  :      Dn1 = Dn2    

Le componenti Normali (Perpendicolari) delle induzioni D e B non cambiano nel passaggio da un mezzo ad un altro sono continue.

Una importante eccezione a queste condizioni si ha nel caso in cui uno dei due materiali è un conduttore perfetto (resistività=0 conducibilità=∞).In questi conduttori infatti a causa dell’effetto pelle la corrente scorre tutta in uno strato superficiale del metallo di spessore infinitesimo (Si è visto che in un conduttore reale o ideale dopo 10^-19 secondi tutte le cariche vanno in superficie) di conseguenza per un conduttore ideale tutti i campi interni alla superficie sono nulli,e la densità superficiale di corrente tende a diventare infinita sulla superficie del materiale. Se il Campo Elettrico è nullo all’interno del conduttore,la continuità del campo tangente sul contorno fa si che il campo Elettrico sia nullo anche al di fuori del materiale.

Et1=Et2=0                  Dn =  ρ                   Bn1=Bn2= 0

Su un conduttore ci sono cariche superficiali e correnti superficiali, Il campo Elettrico è tutto Normale, mentre il campo Magnetico è tutto Tangente.

Queste relazioni possono essere scritte in forma vettoriale :

 n x E = 0                  n · D = ρs

n x H = Js                n · B = 0

LE CONDIZIONI AL CONTORNO POSSONO RIASSUMERSI NEL SEGUENTE MODO:

Et  ed Ht  continue in un dielettrico

Et = 0  ed  J = n x Ht  nel caso del metallo