DIPOLO HERTZIANO

Consideriamo una sorgente elementare di corrente infinitesima,cioè molto piccola,dove la corrente può essere pensata costante:

Si consideri un sistema di riferimento cartesiano, al cui centro c’è un cilindretto di lunghezza dL,all’interno vi percorre una densità di corrente (J) sinusoidale del tipo : J = J0 cos (ωt)   che può essere scritta :

J = J0 Re [e ^+jωt ]

Si ha dunque un conduttore percorso da una corrente costante che oscilla sinusoidalmente. Calcoliamo il Campo Elettromagnetico irradiato in un punto (P).

POSTULATO : Se si riesce a calcolare il campo elettromagnetico in un punto (P) dovuto ad un elemento infinitesimo di corrente, in teoria si sarà in grado di risolvere qualsiasi problema di radiazione.Infatti avendo a che fare con un elemento lunghissimo percorso da una distribuzione di corrente,lo si segmenta in tanti elementi infinitesimi,e se ne calcola il campo elettromagnetico di ognuno successivamente si integra ottenendo il campo totale,qualsiasi distribuzione la si può pensare come sommatoria dei contributi di ogni elemento di corrente.

Il sistema in esame ha simmetria cilindrica, si sceglie di utilizzare un sistema di riferimento in coordinate sferiche, perciò il punto (P) avrà coodinate P(r φ,θ) , il potenziale vettore vale:

A(t) =  μ \ 4π ∫∫∫ [J e^{-j K R} \  r ] dV                A(t) =  μ \ 4π r ∫∫∫ [ J e^{-j K R} ] dV  

In questo caso la distanza (r) è costante per le considerazioni fatte precedentemente, e perciò può essere portato fuori dall’integrale,la corrente (J) va calcolata nell’istante (t-r\v) :

A(t) =  μ \ 4π r ∫∫∫ [J [ t - r \ v] dV

Il potenziale vettore è diretto lungo (z) e verso l’alto come la corrente (J), risolvere l’integrale non è difficile, ricordando che (V) indica un volume qualsiasi che contenga le sorgenti (cilindretto) mentre dV sarà uguale a  dS · dL  (dS sezione dL lunghezza) mentre sappiamo che :

dV = dS · dL              ∫ J  ·  dS   =   I

Otteniamo allora che la soluzione dell’integrale lungo z vale :

A(t) =  μ \ 4π r ∫∫∫ [J [ t - r \ v] dS dL             A(t) =  (μ \ 4π r) I [ t - r \ v] dL az

Il versore (az) serve per ricordare che il vettore (A) è diretto lungo z

Considerando una corrente che oscilla : I = I0 cos (ω t)

A(t) =  (μ \ 4π r) I0 dL cos [ ω (t - r \ v)] az        ovvero       A(t) =  (μ I0 dL \ 4π r) cos [ ωt – β r)] az       

Dove β = ω \ v = 2 π \ λ   il termine  β rappresenta la parte reale della costante di propagazione K.

Conclusioni :  Trovato il potenziale (A) è possibile ora determinare il campo H = 1\ μ  ÑxA

Decidendo di lavorare in coordinate sferiche, si avranno i relativi termini :

Hr = 1\ μ [ ÑxA ] r            Hθ = 1\ μ [ ÑxA ]θ                  Hφ = 1\ μ [ ÑxA ]φ

Per risolvere il rotore di (A) bisogna prima conoscere le sue  relative componenti (Ar,Aθ,Aφ ) :

A φ = 0             Il potenziale vettore A non ha componenti lungo φ

Ar = A cos θ    Componente di A lungo r

A θ = -A sin θ  Componente di A lungo θ

Ora possiamo risolvere le equazioni :

[ÑxA]r  = μ Hr                        [ÑxA]r = 1\ r sen θ  [ ∂ \ ∂ θ ( sen θ A φ) - ∂ Aθ \ ∂ φ ]

Ricordando che (A) non ha componenti lungo φ otteniamo : [ ÑxA ]r = 0  Il campo H non ha comp.radiali

[ÑxA]θ  = μ H θ                        [ÑxA] θ = (1\ r sen θ)   ∂Ar \ ∂ Aφ  -  (1 \ r)  ∂(r Aφ )\ ∂r

Ricordando che A φ = 0 e perciò   ∂Ar \ ∂ Aφ  = 0    si ha : [ ÑxA ]θ = 0  Il campo H non ha comp.lungo θ

[ÑxA]φ  = μ H φ                        [ÑxA]φ = 1\ r [ ∂(r Aθ) \ ∂ r  - ∂ Ar \ ∂ θ ]

Il campo H avrà una componente lungo φ.

Hr = 0

Hθ = 0

Hφ = 1\ μ [ÑxA]φ   Hφ = I dL senθ\ 4π [ - (ω (sen ω t1) \ rv) +  (cos (ω t1) \ r² ) v.pag 175

Il campo magnetico Hφ è formato da una serie di circonferenze concentriche all’asse (z), inoltre tale campo è proporzionale alla corrente ed alla lunghezza dell’elemento di corrente. H è max. sul piano  (θ = π\2) sull’asse θ=0 non c’è campo H. Nell’espressione è possibile notare due termini : un termine che per r→∞ va a 0 come 1\r (RADIAZIONE)e l’altro come 1\r² (INDUZIONE) questo significa che allontanadoci dalla sorgente  il termine (cos) va a zero prima del termine (sen).

A grande distanza predominerà il termine con  1\r

A piccola distanza predominerà il termine con 1\r²  e\o  1\r³                

Nel caso in cui i termini sono uguali ci troviamo a distanza λ\2π Ovvero λ\6 confine tra campo vicino e lontano

Questo significa che a distanza > λ\6 prevalgono i termini di RADIAZIONE (campo irradiato che arriva a grande distanza), ci troviamo in campo lontano

Mentre a distanza < λ\6  prevalgono i termini di campo vicino, INDUZIONE (nelle vicinanze della sorgente vi è una forza elettromotrice indotta, energia reattiva).

Conclusioni :  Trovato campo (H) è possibile ora determinare il campo (E) ricavandolo da (H) :

Ñ x H =  ε ∂E\∂t ( il termine J è assente perche il mezzo non è conduttivo perciò σ = 0 )

In tutto lo spazio quindi il campo E è proporzionale al rotore H, il campo E sarà :

E = 1\ ε ∫ (Ñ x H) dt

Risolvere l’integrale non è complicato, però bisogna come nel caso prec. Conoscere [ÑxH]r [ÑxH]θ  [ÑxH]φ 

Successivamente si integra il rotore trovato ed infine si ottengono le relative componenti del campo (E):

ponendo t 1= t-r\v) tempo ritardado si ha :

Eθ = I dL senθ\ 4πε [ - ω sen (ωt1) \ rv) +  (  cos(ωt1) \ r² v) - (  sen(ωt1) \r³)  

Er = 2I dL cosθ\ 4πε [(  cos(ωt1) \ r² v) + ( sen(ωt1) \r³ )]                  

Eφ = 0

Il campo E ha due componenti (Eθ), (Er), il campo (Eθ) è max a 90° mentre il campo radiale (Er) è max. a 0° (cioè sull’asse del dipolo),

IMPORTANTE : Per capire cosa succede quando si è nella zona di RADIAZIONE, campo lontano cioè a distanze >> λ\6 ,bisogna riconsiderare le equazioni dei campi (H) ed (E) trascurando e quindi eliminando i termini che vanno come  1\r²  1\r³  ottenendo quindi I relativi risultati :

IPOTESI   r >> λ\6   :             Hφ =  - ω I dL senθ\ 4π r v (sen ω t1)

                                           Er = 0

                                           Eθ = I dL senθ\ 4πε [ - ω sen (ωt1) \ rv) ]

A grandi distanze rimarranno soltanto le componenti di (E) lungo θ e le componenti di (H) lungo φ:

Si consideri una sfera attorno al dipolo in esame :

Il campo si propaga nella direzione radiale,dunque dal dipolo partono onde elettromagnetiche in tutte le direzioni, tranne cha nella direzione θ = 0 . In un punto generico P risulta che il campo elettrico è diretto lungo (θ) e il campo H è diretto lungo φ, il campo E ed H sono ortogonali alla direzione r.

POSTULATO : Ricordiamo che la definizione del vettore di Poynting P = E x H , se E è diretto lungo θ ed H lungo φ, allora il vettore di Poynting P è diretto lungo r : Pr = Eθ x Hφ Dunque l’onda si propaga radialmente Eθ ┴ Hφ ed entrambi perpendicolari alla direzione di propagazione, tutto ciò ricorda l’onda PIANA, il campo irradiato da una sorgente di lunghezza infinitesima, a grande distanza (r > λ\6) si comporta quasi come un onda piana. In precedenza abbiamo visto che l’onda piana aveva le seguenti caratteristiche :

1)    E ed H perpendicolari tra loro e perpendicolari alla direzione di propagazione

2)    E ed H in fase nel tempo

3)    E ed H costanti lungo r

4)    il rapporto E \ H ci da l’impedenza d’onda del mezzo

Infatti eseguendo il rapporto Eθ ed Hφ otteniamo proprio (η), l’unica differenza rispetto ad un onda piana è che E ed H invece di essere costanti lungo (r) tendono a zero come (1 \ r)condizione di Sommerfeld . comunque possiamo dire che la nostra onda in esame alla distanza r0 si comporta proprio come un onda piana, perciò possiamo considerare allo stato pratico che ad una certa distanza (r > λ\6) abbiamo a che fare con un onda piana.

POTENZA ASSOCIATA:

Cerchiamo di capire ora quanta potenza è associata all’onda generata dal nostro dipolo, abbiamo esaminato che il vettore di POYNTING fornisce la densità di potenza associata ad un onda elettromagnetica, tale densità integrata in un volume chiuso,ci da la potenza.quindi per vedere quanta potenza si allontana dal dipolo irradiante è necessario determinare P :

P = E x H

Pθ = - Er x Hφ            Pr = Eθ x Hφ

Il vettore di Poynting ha due componenti una lungo (θ) e l’altra lungo (r) , possiamo capire che (Pr) esprime una radiazione radiale, mentre (Pθ) oscilla (va su e giu).Conoscendo le componenti dei campi trovate prima, è possibile esprimere entrambe i prodotti.

POSTULATO : Dalla risoluzione del prodotto Pθ = - Er x Hφ notiamo che tale potenza è tutta intorno alla sorgente ed il valore medio vale zero (Pθ integrato in un periodo T ci da Pm = 0), è importante notare che tale potenza ha valor medio nullo, è potenza che rimane attorno alla sorgente continuando ad andare su e giu, questa potenza non viene dissipata ne irradiata, è quella che normalmente si indica con energia REATTIVA immagazzinata intorno alla sorgente. Invece dalla risoluzione di Pr = Eθ x Hφ possiamo notare che il valor medio è positivo e quindi  > 0 questo significa che solo le componenti Eθ ed Hφ considerati in campo lontano (1\r) forniscono una potenza a valor medio non nullo, e quindi solo a questi è associata una potenza irradiata :

Pr_med = 1\2 (E² θ_radiativa \ η )      [w\m²]

La densità di potenza irradiata non sarà uniforme ma sarà max. per θ = π\2 e nulla sull’asse (θ = 0)

Una volta determinato Pr_med per determinare la potenza totale irradiata bisogna integrare attraverso una sfera ad (r) costante e centro nell’origine che racchiude uno strato di radiazione :

W = ∫∫  Pr_med  dS

Si deve perciò considerare l’elemento di superficie di una sfera (dS = 2πr senθ r dθ) ,attraverso poi l’integrazione si ottiene la potenza, che non dipende dal raggio della sfera,in quanto questo termine nei calcoli viene semplificato.

Si ottiene perciò :                  W = 80 π² (dL\λ)²  I² eff                  con Ieff= I\√2

Cerchiamo di capire però chi è che fornisce la POTENZA irradiata (W); in realtà sappiamo che per alimentare un  antenna si utilizza un Generatore il quale fornisce una certa corrente,a sua volta il generatore si vedrà assorbire una potenza da parte dell’antenna che poi verrà irradiata nello spazio circostante, questo significa che l’antenna si presenta al generatore come un carico.

E’ possibile quindi definire una RESISTENZA DI RADIAZIONE che rappresenta la nostra Antenna, è evidente perciò che questa resistenza moltiplicata per la corrente (I² eff) ci darà proprio la Potenza che il generatore fornisce all’antenna e che poi a sua volta irradia nello spazio :

RESISTENZA DI RADIAZIONE :            Rrad = 80 π² (dL\λ)²     con  dL = 2h

Per essere piu chiari dobbiamo dire che la nostra antenna non rappresenta un pura resistenza, ma anche una reattanza che può essere induttiva o capacitiva, questo perche c’è energia reattiva :

Riassumendo possiamo dire che un elemento che irradia è visto dal generatore come un circuito RX, dove R è la resistenza di radiazione che tiene conto della potenza assorbita ed irradiata, mentre la X tiene conto di tutta l’energia Reattiva che oscilla lungo (θ) senza però essere irradiata.

Un altro concetto importante è capire quale percorso fa la corrente, sappiamo che prendendo un antenna molto corta ed alimentandola con un generatore, la corrente assumerà un valore nullo nelle posizioni terminali,mentre per il resto  del percorso all’interno dell’antenna non si sa come andrà e quale valore assume :

Ipotizzando che la corrente lungo (z) fosse costante l’andamento è figurato dal secondo grafico, ma un elemento radiante non può avere corrente costante perchè essa fisicamente deve annullarsi alle estremità, perciò la situazione reale è figurata nella terza figura dove la corrente presenta tratti di crescenza e di decrescenza, nulla agli estremi e max. in un punto. Purtroppo che l’andamento sia rettilineo non si sa di preciso, comunque possiamo dire che se la lunghezza dell’elemento radiante (L) è molto corta rispetto alla lunghezza d’onda (λ) è possibile approssimare la corrente con un andamento rettilineo.

IMPORTANTE: i conti fatti precedentemente si riferivano ad una struttura dove la corrente era costante (il calcolo dell’integrale è valido solo nel caso I = cost lungo Z) avendo un andamento rettangolare (che comunque si annullava agli estremi), in realtà però la corrente ha un andamento triangolare è quindi se da una distribuzione rettang. Si passa a quella triang. La potenza irradiata va divisa per 4 :

W = [80 π² (dL\λ)²  I² eff ]  1\4              W = 200  (dL\λ)²  I² eff            w = R_rad  I² eff

ESEMPIO : calcolare la resistenza di un Antenna corta, di lunghezza (h) posta su un piano di massa :

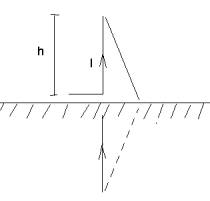
Tenendo presente il principio delle immagini è sufficiente farne l’immagine, riconducendoci al caso precedente, anche se in realtà l’antenna irradia solo sul piano superiore, si ottiene quindi :