|
La nascita di una nuova scienza La teoria del caos, la cui nascita è legata a celebri figure, come Feigenbaum, Lorenz, Dyson, e Smale, si sviluppa con l'intento di trovare una spiegazione "scientifica" a un'ampia gamma di fenomeni troppo a lungo trascurati dai fisici, dalla turbolenza nei liquidi e nei gas, al cambiamento delle condizioni atmosferiche, alle fluttuazioni delle popolazioni animali e vegetali, alle oscillazioni degli impulsi provenienti dal cuore e dal cervello, alla Grande Macchia Rossa di Giove, alle variazioni dei prezzi delle merci. Se nell'Unione Sovietica i primi studi sul caos risalgono già agli anni '50, si deve aspettare almeno un decennio affinchè questa nuova teoria si sviluppi anche nel panorama occidentale. Quando Feigenbaum comincia le sue ricerche negli anni Settanta, gli scienziati che si occupano del caos sono ancora molto pochi, spesso ostacolati nel loro lavoro dai difensori della fisica tradizionale, spaventati da idee così nuove e fondate su una matematica che sembra difficile e anticonvenzionale. Dagli anni Ottanta, quello del caos è diventato un settore in continua espansione, fondato su una ricerca ininterrotta e coordinata dal Center for Nonlinear Studies.
|
||
| Oltre la
fisica classica
Quali sono i veri "meriti" della teoria del caos?
Poste tali premesse, è facile capire perchè la Teoria del caos è stata considerata come la terza grande rivoluzione della Scienza, dopo la Teoria della relatività einsteiniana e la Meccanica quantistica, con la seguente precisazione:
Se è vero che lo studio del caos ha messo in discussione il principio di prevedibilità, dall'altro ha mostrato come molti sistemi definiti "aleatori" siano più prevedibili di quanto si pensi e possano essere spiegati in termini relativamente semplici.
|
||
| L'esperimento
di Lorenz
Edward Lorenz viene solitamente ricordato per gli studi effettuati sulle previsioni delle condizioni meteorologiche, analizzate da un punto di vista matematico. Il suo esperimento, dovuto anche alla presenza di un fattore accidentale, si svolge nelle seguenti fasi:
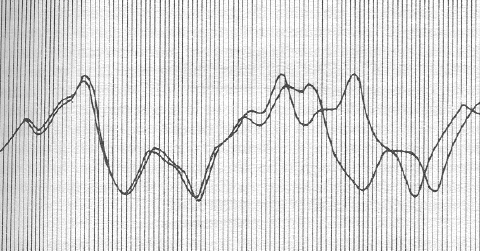
- Ogni minuto la macchine segna il trascorrere di un giorno stampando una serie di numeri su una pagina; per qualche ragione misteriosa, nulla accade due volte nella stessa maniera. - Lorenz elabora una sorta di grafica primitiva: sceglie una variabile, come la direzione dei venti e, su tale base, fa stampare al computer una linea curva continua, formata dalla ripetizione della lettera "a" e da un certo numero di spazi vuoti. - Lo scienziato decide di analizzare lo stesso processo partendo dalla metà: fornisce al computer le condizioni iniziali tratte dallo stampato precedente approssimandole a tre cifre (Lorenz ritiene che tale arrotondamento non abbia influenze rilevanti, sulla base del principio classico secondo il quale "le influenze piccolissime possono essere trascurate e influenze piccole a piacere non vengono mai ad assumere effetti grandi a piacere"). - I risultati smentiscono le previsioni, dal momento che le condizioni meteorologiche ottenute in questo modo divergono molto dall'andamento della fase precedente (inizialmente si ha una convergenza quasi perfetta tra le due curve, poi una appare leggermente in ritardo, in seguito lo sfasamento è più evidente e alla fine la somiglianza è totalmente scomparsa).
|
||
| L'effetto
farfalla
Per colpa di un chiodo si perse lo zoccolo; per colpa di uno zoccolo si perse il cavallo; per colpa di un cavallo si perse il cavaliere; per colpa di un cavaliere si perse la battaglia; per colpa di una battaglia si perse la guerra.
|
||
| L'attrattore
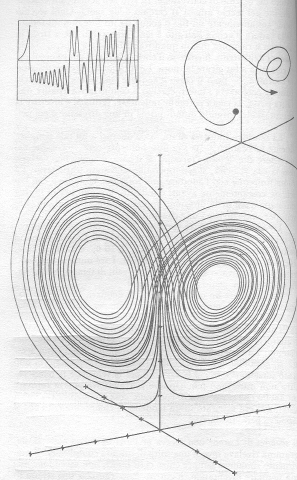
di Lorenz
L'esperienza di Lorenz dà il via alla ricerca di una lunga serie di "attrattori strani", come quelli di Hénon e di Rossler, disegnati attraverso particolari tecniche di visualizzazione. Al di là delle apparenti differenze tutti gli attrattori caotici, costituiti da linee infinite racchiuse in are finite, sono frattali, oggetti che rivelano dettagli sempre maggiori via via che vengono ingranditi. Il caos dunque, genera frattali in modo naturale.
|
||
| Stiratura e
piegamento dello spazio degli stati
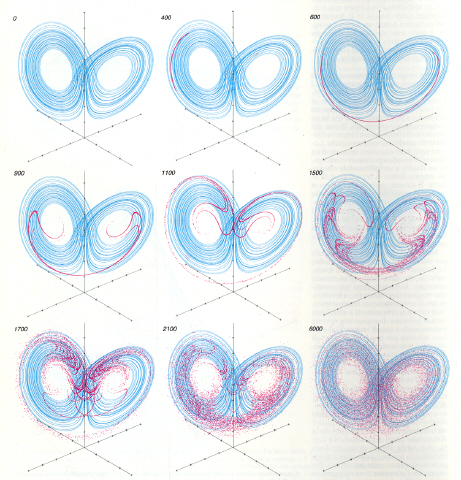
La differenza tra gli attrattori strani e quelli che descrivono sistemi non caotici è evidente: mentre in questi ultimi le orbite vicine tra loro restano tali anche a distanza di tempo (rendendo possibile una previsione a lungo termine), negli attrattori caotici due orbite corrispondenti a condizioni iniziali prossime divergono in modo esponenziale Si può comprendere facilmente la natura di un attrattore caotico pensando a un'operazione di stiratura e piegamento dello spazio degli stati. La divergenza esponenziale delle orbite è. Infatti, un fenomeno locale. Nella realtà, dal momento che la dimensione dgli attrattori è finita, due orbite non possono continuare a divergere all'infinito e l'attrattore è costretto a ripiegarsi su se stesso. Proprio nell'intento di misurare lo stiramento, la contrazione e il piegamento dello spazio delle fasi di un attrattore sono stati introdotti gli esponenti di Ljapunov. Se un esponente > 0 indica uno stiramento, a un esponente < 0 corrisponde una contrazione. E' facile, quindi, prevedere che: - il punto fisso è descritto solo da esponenti negativi; - il ciclo limite è rappresentato da un esponente nullo e da esponenti negativi; - in un attrattore caotico almeno un esponente è positivo. Il fatto che un attrattore caotico derivi, come dimostrato da studi topologici, dalla stiratura e dal piegamento dello spazio degli stati consente due ordini di osservazioni, inerenti all'evoluzione del sistema e alla sua imprevedibilità.
|
||
| Attrattori
caotici e indeterminazione
Gli attrattori caotici si comportano, quindi, come una sorta di pompa, in quanto portano a manifestazione macroscopica le fluttuazioni microscopiche (ecco il vero significato di "dipendenza dalle condizioni iniziali"!). Se il loro effetto è simile a quello degli amplificatori di rumore, si differenziano da questi ultimi in quanto il comportamento caotico del sistema è indipendente dal livello di rumore iniziale il quale, a sua volta, è dovuto solo all'imprecisione delle misurazioni. In altre parole, i sistemi caotici generano aleatorietà di per sè, senza bisogno di un apporto esterno.
|
||
|
La cella di Couette e il moto dei fluidi Il fatto che i fenomeni meteorologici studiati da Lorenz nascondano un struttura frattale non fornisce, in realtà, certezze di alcun tipo in merito all'aleatorietà dei sistemi fisici. In altre parole, occorre dimostrare che gli attrattori strani sono alla base di tutti i sistemi considerati caotici. Un importante contributo viene fornito in questo senso da Gollub e Swinney e dai loro studi sul moto dei fluidi, condotti attraverso la Cella di Couette. I due ricercatori utilizzano un dispositivo relativamente semplice: lo spazio tra due cilindri concentrici è occupato da un fluido e uno o entrambi i cilindri vengono fatti ruotare con una certa velocità angolare. Si misura, infine, la velocità del fluido in un dato punto al variare nel tempo della velocità di rotazione dei cilindri. I dati raccolti vengono in seguito riportati su un grafico.
|
||
| Conclusioni
L'introduzione della Regola di Takens consente i riesaminare il moto dei fluidi esaminato da Gollub e Swinney e di ottenere dalla ricostruzione dello spazio degli stati proprio un attrattore caotico. Negli ultimi anni, diverse ricerche hanno dimostrato che numerosi sistemi dinamici presentano un'aleatorietà dovuta a un attrattore caotico. Il fatto che nei grafici sia possibile individuare determinate strutture, che si ripetono qualunque si il fenomeno studiato, dimostra che l'aleatorietà presenta una base deterministica. Quando si parla di "caos deterministico" si intende proprio un caos generato da regole fisse, le quali non contengono di per sè alcun elemento casuale. Ecco la ragione per la quale sempre più spesso, più che di "caos", si preferisce parlare di "complessità".
|
||
| La scienza
del caos e le sue applicazioni
La teoria del caos è ancora lontana dall'aver trovato una sistemazione definitiva. Sistemi caratterizzati da molti gradi di libertà, infatti, potrebbero dar luogo a un comportamento aleatorio nel vero senso del termine e alcune configurazioni spaziali in movimento, come le dune del Sahara, potrebbero anche non essere descritte efficacemente da un unico attrattore in un unico spazio degli stati. Tuttavia, è ormai un dato certo che gli studiosi del caos hanno allargato le frontiere della conoscenza umana, consentendo un approccio del tutto originale a discipline quali l'Astronomia, la Psichiatria e la Cardiologia.
|
||
| Altre informazioni relative all'approfondimento e al modo in cui si è strutturato l'approfondimento nel tempo si possono trovare consultando le pagine del blog che abbiamo costruito con il mio insegnante di fisica. Ecco di seguito il link: http://nuovocaos.blogspot.com/ | ||
| Sara Nuovo Classe 5B | ||