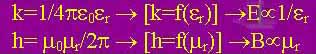APPROFONDIMENTO TEMATICO DI FISICA di Sara Vecchio

Le quattro interazioni fondamentali della materia

 Origine dei fenomeni gravitazionali, elettrici e magnetici e cenni storici

La scoperta di un’interazione fra le masse risale al 1684, quando Isaac Newton ebbe l’intuizione di confrontare due fenomeni apparentemente diversi come la caduta dei corpi sulla Terra e il moto di rivoluzione della Luna attorno alla Terra, e ne suppose la comune origine.

La formulazione della legge che riguarda l’interazione elettrostatica si deve invece a Charles Augustine de Coulomb, che tra il 1785 e il 1789 condusse una serie di accurati esperimenti utilizzando una bilancia a torsione unifilare (simile concettualmente a quella di Cavendish) con cui confermò la sua ipotesi teorica.

Una prima corroborazione empirica della teoria newtoniana si ebbe invece solo nel 1798 proprio ad opera di Henry Cavendish, il quale riuscì a misurare (mediante un dispositivo analogo a quello utilizzato da Coulomb) la forza di attrazione gravitazionale tra oggetti di massa relativamente piccola (se confrontata con gli ordini di grandezza dell’astronomia) e ricavò sperimentalmente un valore della costante G molto vicino a quello previsto da Newton in base ad una stima della densità della Terra.

Il mistero che avvolgeva il magnetismo cominciò a dissolversi solo nel 1600 con William Gilbert, il primo a intuire che l’orientarsi di un ago magnetico dipendeva dal magnetismo della terra stessa. Formulazioni matematiche delle leggi del magnetismo, fenomeno presto conosciuto e sfruttato nella navigazione, non se ne ebbero fino al XIX secolo.

La struttura matematica della legge

La legge elettrostatica di Coulomb ( F=k q₁q₂/r² ) e quella gravitazionale di Newton (F=G m₁m₂/r²) hanno un'analoga struttura matematica: per entrambe l'intensità della forza è, nel caso di corpi puntiformi, direttamente proporzionale al prodotto dei valori di una grandezza fisica corrispondente ad una proprietà posseduta dai due corpi in relazione (rispettivamente l'intensità di elettrizzazione e la massa gravitazionale) ed è inversamente proporzionale al quadrato della distanza che separa i due corpi. La somiglianza della forma matematica, in particolare la proporzionalità inversa al quadrato della distanza, determina la generica somiglianza del vecchio modello rutherfordiano dell'atomo e di quello planetario, dove le interazioni newtoniana e coulombiana agiscono come forza centripeta rispettivamente sui pianeti e sugli elettroni determinando la stabilità dell'atomo e del sistema solare (e dunque la chiusura) delle loro orbite. Simile è la struttura matematica della legge magnetostatica di Coulomb  (F=µ p₁p₂/r²) ma tale formula ha poco valore per il carattere prettamente teorico del concetto di carica magnetica, data l'impossibilità di isolare i poli magnetici. La legge che caratterizza l'interazione magnetica vera e propria è invece legata alla forma della sorgente; ma secondo la generalizzazione proposta da Laplace si ricava F=hsinßq₁v₁q₂/r²), e dunque sempre una struttura del tipo y=k/x².

Il raggio d'azione delle interazioni

Elemento comune alle tre interazioni è un raggio d'azione teoricamente infinito, contrapposto a quello estremamente limitato delle due interazioni nucleari, debole e forte (rispettivamente di raggio d’azione <<10^-15 m e <10^-15 m).

Attrazione e repulsione dell’interazione

A livello macroscopico, tutti i corpi aventi massa si attraggono ma non tutti i corpi aventi cariche (elettriche, magnetiche, di colore o deboli) si attraggono.

Il campo gravitazionale è generato da masse, quello nucleare debole da cariche deboli, quello nucleare forte da cariche di colore e quello campo elettromagnetico da cariche elettriche (il campo elettrostatico è generato da cariche elettriche in quiete, un campo magnetico è sempre e comunque generato da cariche elettriche in moto).

La massa c’è di un solo segno, la carica (elettrica e magnetica) di due. Questo ha conseguenze notevoli sulle caratteristiche delle interazioni.

Un corpo esteso è in genere elettricamente neutro, perché a livello macroscopico la concentrazione dei due tipi di carica è pressoché uguale [1] (ossia la somma algebrica della carica è zero): l’interazione elettromagnetica (in quella magnetica i due poli opposti non sono distinguibili neppure a livello microscopico), nonostante l’esteso raggio d’azione riveste dunque un ruolo fondamentale solo nell’equilibrio “microcosmico” (ma a livello subatomico viene poi scalzata dalle interazioni nucleari).

Le debolissime forze gravitazionali, solo attrattive, che si esercitano tra le singole particelle di un corpo si sommano invece fino a produrre una forza intensa tra le enormi concentrazioni di massa presenti nell’universo.

Al contrario l’interazione forte, benché sia sempre di tipo attrattivo, poiché ha un raggio d’azione molto breve e si manifesta solo tra quark o adroni, non si rivela che a livello subnucleare.

Considerazione: a priori ogni particella non elementare può essere soggetta a tutte le interazioni, eccetto che per l’interazione forte.

L’influenza del mezzo

Mentre G è costante, k e h variano a seconda del mezzo [2] in cui si trovano i corpi, e in particolare k ha nel vuoto il suo valore massimo, mentre h può anche assumere valore maggiore che nel vuoto[3] (nei materiali paramagnetici o ferromagnetici):  

_{Nel caso gravitazionale, come nel caso delle interazioni, qualunque mezzo interposto sarebbe un altro corpo soggetto alla forza (tutti i corpi hanno massa e, nel nucleo, l’unico mezzo “interponibile” tra due particelle è una terza particella). Non ha dunque senso parlare di mezzo interposto.Nel caso elettrico, l’influenza del mezzo è determinata dal fenomeno della polarizzazione. Un campo elettrico altera la distribuzione delle cariche nelle molecole: i nuclei vengono spostati nel senso delle linee di forza, mentre la nuvola elettronica si sposta in senso opposto; la struttura ordinata di dipoli indotti o naturali orientati che ne deriva genera a sua volta un campo elettrico opposto a quello che ha prodotto la polarizzazione, per cui il campo totale risulta sempre più debole di quello che si avrebbe nel vuoto (la costante dielettrica relativa è sempre < 1).L’analogo della polarizzazione nel caso magnetico è il diamagnetismo: tutte le sostanze presentano la proprietà di reagire in opposizione al campo d’induzione magnetica ad esse applicato [4], ma il controcampo è molto piccolo (la permeabilità magnetica relativa è di poco minore dell’unità) e non dipende dal campo applicato, né dalla temperatura. Fenomeni opposti al diamagnetismo sono il paramagnetismo e il ferromagnetismo, in cui le sostanze si magnetizzano nello stesso verso del campo inducente: ma mentre nel primo caso la permeabilità magnetica relativa assume valori di poco superiori ad uno e aumenta al decrescere della temperatura, per i materiali ferromagnetici si ha un apermeabilità magnetica relativa fino a cinque ordini di grandezza superiore all’unità che cresce con l’intensità del campo magnetico esterno e decresce con l’aumentare della temperatura [5].}

_{Confronto dei valori delle costanti (nel SI)}

_{Mentre la costante gravitazionale G ha un valore molto piccolo, la costante elettrica k e quella magnetica h sono molto grandi}

G= (6,6726±0,0006)·10^-11 Nm²/Kg²

k_vuoto=8,99·10⁹ Nm²/C²       e₀= (8,854187818±0,000000008)·10^-12 C²/Nm²

h_vuoto=2·10⁷  Tm/A      m₀=4p·10⁷ Tm/A

Il fatto che per m₀ sia stato fissato un valore, mentre G ed e₀ sono stati misurati, dipende dalla circostanza che l’ampere, unità si misura nel Sistema Internazionale dell’intensità di corrente, è definita con un procedimento di misura che utilizza un fenomeno magnetico (e quindi forze di tipo magnetica nella cui espressione compare m₀).

Esistenza o meno di schermi all’interazione

I modi di schermare ciascun campo sono in realtà più una differenza che un’analogia. All'interno di un conduttore cavo (superficie chiusa) il campo elettrico è nullo ; un conduttore in condizioni di equilibrio è per forza equipotenziale in ogni suo punto (una differenza di potenziale comporterebbe un moto di cariche fino all'annullamento della stessa) e dunque in tutto il suo spessore il campo elettrico è nullo. Ma la prima affermazione è ancora più vera se il conduttore fosse cavo; sia in un corpo continuo che in un corpo cavo contenente cariche , le cariche si distribuiscono sulla superficie esterna: non possono allora esserci linee di forza nella cavità perché non ci sono cariche che ne siano pozzi e sorgenti (per le considerazioni precedenti, il campo è nullo sulla superficie interna del conduttore).
Un qualsiasi campo esterno influisse su tale situazione di equilibrio, ma il moto delle cariche libere sulla superficie del conduttore riporta il sistema all'equipotenzialità (e dunque l'assenza di campo) con il raggiungimento di una nuova distribuzione delle cariche. Un conduttore cavo agisce dunque come schermo per il campo esterno.
schermo completo(gabbia di Faraday).
Uno strato sferico non esercita su un punto materiale situato al suo interno neppure forza gravitazionale , ma già se la forma del corpo cavo è differente l'analogia scompare per l'inesistenza di un'induzione gravitazionale: le molecole o gli atomi, pur sotto l'effetto di una differenza di potenziale, non possono muoversi per i vincoli che li legano assieme e dunque il sistema non è in grado di raggiungere automaticamente una posizione di equilibrio ; inoltre è il doppio segno delle cariche che permette al sistema di raggiungere l'equilibrio (di annullare il campo esterno nel conduttore) con il moto dei soli elettroni, mentre la massa è di un segno solo. Parlando degli schermi per l'esterno contro l'azione del campo interno a queste motivazioni si aggiunge il fatto che non esiste un fenomeno analogo a quello elettrico di "messa a terra" (sempre per la staticità delle molecole in un solido e l'unicità di segno della massa).
Efficace schermo all'interazione magnetica è un toroide (o una sfera o un qualunque corpo cavo di un certo spessore) di materiale ferromagnetico: caratteristica di questa classe di sostanze è infatti quella di canalizzare le linee di forza del campo, che dunque non passeranno per il centro del corpo considerato. 
Poiché l’interazione gravitazionale è sempre attrattiva e poiché per essa non esiste un fenomeno analogo a quello elettrico di “messa a terra”, non esistono schermi per l’esterno contro l’azione del campo interno (gabbia di Faraday); ma uno strato sferico non esercita alcuna forza gravitazionale su un punto materiale situato al suo interno. Per le interazioni nucleari è la distanza stessa lo “schermo”: a livello subatomico non si può certo parlare di materiale interposto.

Ordine di grandezza dell’interazione

L’intensità relativa delle interazioni, assumendo quella forte come riferimento, risulta:

Natura centrale delle forze

Nei primi due casi la forza agisce lungo la congiungente tra due corpi, o meglio tra i loro centri di massa o tra i loro centri geometrici: infatti come la legge di Newton è applicabile se i corpi hanno dimensioni trascurabili rispetto alle distanze che li separano (e dunque se si può considerare la massa come concentrata in un punto), similmente la legge di Coulomb è valida per cariche puntiformi o per corpi sferici con la carica uniformemente distribuita sulla superficie [6]. La forza che un filo percorso da corrente esercita su un ago magnetico, non è invece diretta secondo la congiungente dei due corpi: nello studio del magnetismo diventa dunque fondamentale una grandezza fisica quale il momento magnetico.

Tipo di orbita aperta o chiusa che ne consegue

Dipende dall’energia del sistema, indipendentemente dall’interazione in gioco. Nel caso di una forza proporzionale al quadrato della distanza si può dimostrare che le orbite planetarie sono ellissi.

Semplificando la situazione al caso convenzionale di orbite circolari compiuta dal corpo di massa minore attorno a quello di massa maggiore, si dice che il secondo imprime un’accelerazione centripeta     al primo. Secondo la legge di gravitazione universale (ma il procedimento è ripetibile anche per le altre interazioni, data l’analogia delle loro formule matematiche) tale accelerazione è e dunque  L’energia totale del sistema, somma algebrica dell’energia potenziale e di quella cinetica, sarà dunque  ossia una quantità negativa.

Nel caso di orbite circolari, la forza attrattiva agisce sul secondo corpo imprimendo un’accelerazione centripeta e dunque per la gravità (il procedimento è ripetibile anche per le altre interazioni data l’analogia delle loro formule matematiche) v=(GM/r)½  E_totale=E_cinetica+E_potenziale=GMm/2r-GMm/r=-GMm/2r .

L’energia totale è negativa anche nel caso di un’orbita ellittica ed è sempre valida l’equazione di sopra, ma assumendo r uguale al semiasse maggiore dell’ellisse: l’energia totale dipende solo dalle dimensioni globali dell’ellisse, ma non dalla sua forma (da cui dipende invece la quantità di moto, maggiore nelle orbite di eccentricità minore). Più grande è l’energia, più grande è il semiasse maggiore: se l’energia tende a zero, l’ellisse tende a chiudersi all’infinito, ossia a degenerare in una parabola; se l’energia è positiva il corpo compie un’orbita aperta di tipo iperbolico.

Natura conservativa delle interazioni

Un campo è conservativo se l’energia posseduta dal corpo dipende univocamente dalla posizione che esso occupa nel campo.

Il campo magnetostatico è conservativo, quello elettrico variabile no!

Note

[1] La presenza di carica in un corpo elettricamente neutro può essere rivelata attraverso il fenomeno di induzione elettrostatica, che altera la distribuzione di equilibrio, o quello della polarizzazione.

[2] I materiali che consentono la propagazione dell’elettrizzazione sono definiti conduttori, quelli che non la consentono sono gli isolanti (o dielettrici). Parlando di interazione coulombiana ci si riferisce a distribuzioni di carica in equilibrio elettrostatico, e dunque il mezzo interposto non deve permettere il moto delle cariche.

[3] Suscettibilità magnetica c=m_r-1

[4] Legge di Faraday-Neumann-Lenz

[5] fino alla temperatura critica della sostanza, il punto di Curie, superata la quale assumono le proprietà paramagnetiche

[6] teorema di Newton e teorema di Coulomb