home

LA GEOMETRIA IPERBOLICA

La geometria iperbolica (dal greco hyperbolé, in eccesso) si sviluppa a partire dalla famosa crisi ottocentesca, e venne sviluppata principalmente da GAUSS, seguito da LOBACEVSKIJ e BOLYAI. Si basa sulla negazione del V postulato di Euclide, ammettendo invece l'esistenza di più parallele ad una retta per un punto dato.

Il postulato diventa: per un punto P non appartenente ad una retta r passano almeno due rette parallele a r. Queste parallele s e t formano un angolo che è tanto più piccolo quanto la distanza del punto dalla retta data è minore. Le rette s e t sono ugualmente inclinate rispetto alla perpendicolare alla r per P.

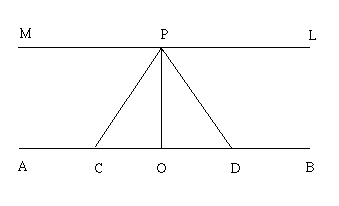
Da questa considerazione sorgono delle conseguenze curiose: le più interessanti sono quelle relative ai triangoli, che sono anche quelle maggiormente comprensibili con una media conoscenza di geometria elementare. Esistono rette che non si incontrano ma non sono parallele: esse sono dette rette non secanti. Alcune delle conseguenze relative i triangoli riguardano la somma dei loro angoli interni. Essa varia, in ragione inversa dell'area, da un minimo di 90° ad un massimo di 180°. In generale, la somma degli angoli interni di un poligono a n lati è minore di 180°(n-2). Inoltre, se due triangoli sono riferiti in modo tale che gli angoli corrispondenti siano congruenti, sono pure congruenti i lati corrispondenti: ovvero, due triangoli con tre angoli congruenti sono anch'essi congruenti (in geometria euclidea si sarebbe parlato di similitudine: qui, invece, non esiste una trasformazione del genere, perché aumentando l'area del triangolo diminuisce la somma degli angoli interni). Ci si può facilmente rendere conto di questo immaginando di disegnare un triangolo sulla superficie interna di un paraboloide, ovvero un solido di rotazione ottenuto da una parabola che ruota attorno al suo asse. Il paraboloide è un buon modello di geometria iperbolica.

I modelli più interessanti di questa geometria sono il modello di Felix Klein e il modello di Henry Poincarè. Essi, nonostante sembrino molto differenti tra di loro, hanno molti punti in comune: anzi è stato dimostrato che sono praticamente la stessa cosa. Il modello di Klein, dato un cerchio k, è così costituito: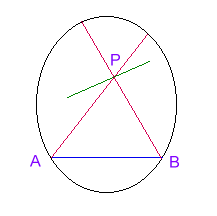

-piano è il cerchio k senza la circonferenza,

-punto è ogni punto appartenente a k ma non alla circonferenza,

-retta è ogni corda di k meno gli estremi che appartengono alla circonferenza.

La circonferenza è definita come luogo dei punti all'infinito del piano, ogni retta fuori da k è immaginaria. È facile verificare che valgono i postulati dal I al IV, e il nuovo V: infatti dato un punto P ed una retta non passante per P, si individua un fascio di rette. Le rette formano un angolo che diminuisce in ragione della vicinanza di P a r.

Il modello di Poincarè prevede invece, data una retta x, questi enti:

-piano il semipiano positivo sopra la x esclusa la x stessa,

-punto ogni punto appartenente al semipiano sopra x esclusa x stessa,

-retta ogni semicirconferenza con centro in x del piano. Anche qui si realizzano tutti i POSTULATI finora ammessi più il V riformulato. Da notare che come rette si considerano anche le perpendicolari alla x, che sono circonferenze con raggio infinito.

LA GEOMETRIA ELLITTICA

La geometria ellittica segue questa linea di pensiero: per un punto non passa nessuna parallela ad una retta data. Questo tipo di geometria è stato sviluppato soprattutto da RIEMANN. Il modello di spazio che segue meglio questa geometria è la sfera ed è qui che ci conviene enunciare le proprietà dello spazio ellittico.

Data una sfera , si definiscono i seguenti enti:

-piano la superficie sferica,

-punto ogni coppia di punti diametralmente opposti della sfera,

-retta ogni cerchio massimo della sfera.

Nello spazio così definito ci sono diverse cose da notare: non tutti i postulati si verificano, infatti il II POSTULATO non si verifica, perché tutte le rette hanno lunghezza definita. Inoltre, poiché si verifica il I POSTULATO, la coppia di punti diametralmente opposti in cui le circonferenze si secano deve essere un solo punto. Siccome una retta non è mai parallela ad un'altra, anche le perpendicolari ad una stessa retta si incontrano in un punto. Dunque tutte le perpendicolari (infinite) ad una retta concorrono in uno stesso punto, e i segmenti staccati tra la retta e il punto sono uguali . La somma degli angoli interni di un triangolo è sempre maggiore di 180° ed esistono triangoli trirettangoli. Per questi, come nella geometria iperbolica, valgono teoremi affini a quelli del piano euclideo.

Un'altra caratteristica notevole del piano ellittico è che esso è unilaterale, cioè non ha due facce. Questo tipo di geometria è utile per descrivere il principio di inerzia di Galileo : un punto su cui la somma delle forze sia nulla è in quiete o si muove di moto rettilineo uniforme lungo una geodetica dello spazio ellittico. Tuttavia questa geometria ha molta meno importanza storica perché è stata scarsamente sviluppata.