|
|
|
|
|
GRADI |
0° |
|
|
|
|
|
135° |
150° |
180° |
270° |
360° |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
RADIANTI |
|
p/10 |
|
|
p /3 |
p /2 |
3p/4 |
5p/6 |
p |
3p/2 |
2p |
 ANGOLO
RETTO (b
=
90°) ANGOLO
RETTO (b
=
90°) |
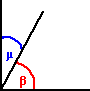 ANGOLI
COMPLEMENTARI (b
+
m
=
90°) ANGOLI
COMPLEMENTARI (b
+
m
=
90°) |
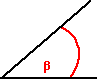 ANGOLO
ACUTO (b
<
90°) ANGOLO
ACUTO (b
<
90°) |
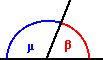 ANGOLI
SUPPLEMENTARI (b
+
m
=
180°) ANGOLI
SUPPLEMENTARI (b
+
m
=
180°) |
|
|
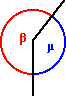 ANGOLI
ESPLEMENTARI (b
+
m
= 360°) ANGOLI
ESPLEMENTARI (b
+
m
= 360°) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
Formule di sottrazione |
|
|
sin(m-b) = sinmcosb - cosmsinb |
|
|
cos(m-b) = cosmcosb + sinmsinb |
|
|
tg(m-b)=(tgm - tgb)/(1 + tgmtgb) |
|
|
ctg(m-b) = (ctgmctgb + 1)/(ctgb - ctgm) |
|
|
Formule di duplicazione |
|
sin2b = 2 sinb cosb |
|
cos2b = cos2b - sin2b = 1 - 2sin2b = 2cos2b - 1 |
|
|
|
|
|
Formule di bisezione |
|
|
|
|
|
|
|
|
|
Formule di prostaferesi |
|
|
|
|
|
|
|
|
|
[con p
e q |
|
[con p
e q |
|
Formule di Werner |
|
sinmcosb
= |
|
cosmcosb
= |
|
sinmsinb
= |
|
Espressione di sinb, cosb, tgb, ctgb, in funzione razionale di tg(b/2) |
|
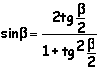 |
|
|
|
|
Relazioni
tra gli elementi di un triangolo rettangolo b = c
tgb c = b
ctgb
|
Teorema della corda |
|
AB = 2r sinb |
Teorema
dei seni (o di Eulero) Teorema
delle proiezioni a = b
cosg
+ c cosb b = a
cosg
+ c cosa c = a
cosb
+ b cosa
![]()
|
Teorema del coseno (o di Carnot) |
|
a2 = b2 + c2 - 2 bc cosa b2 = a2 + c2 - 2 ac cosb c2 = a2 + b2 - 2 ab cosg |
|
Teorema di Nepero |
|
|
|
Formule di Briggs |
|
|
|
|
|
|
|