Enigmi e Test

Il volo attorno al mondo

Un gruppo di aerei è dislocato su una piccola isola. Il serbatoio di ogni aereo contiene esattamente carburante sufficiente a consentirgli mezzo giro del mondo, ma è possibile trasferire quanto carburante si vuole dal serbatoio di un aereo a quello di un altro mentre gli aerei sono in volo. La sola fonte di carburante è sull'isola e si suppone che non venga perduto tempo nel rifornimento sia in aria che al suolo. Qual è il numero minimo di aerei necessario per assicurare il volo di uno di essi per un giro completo attorno al mondo, ammettendo che gli aerei abbiano la stessa velocità costante rispetto al suolo, lo stesso consumo di carburante e che tutti gli aerei rientrino sani e salvi alla base?

In autostrada

Percorrendo un tratto autostradale alla velocità costante di 120 km/h, un automobilista sorpassa, in 30 minuti, 50 camion che a loro volta marciano a una velocità di 80 km/h. Ora, supponendo costanti tutte le velocità in gioco e soprattutto mentenendo costanti i flussi di traffico, quanti camion percorrono quell'autostrada in un'ora? In poche parole un'ipotetica persona ferma al lato della strada quanti camion vedrebbe passare davanti a sè in un'ora?

La diagonale del rettangolo

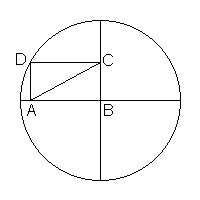Un rettangolo è inscritto in un quadrante di cerchio come mostrato in figura. Determinate con esattezza la lunghezza della diagonale AC, sapendo che il cerchio ha raggio unitario.

Le 1000 lire mancanti

Ci sono tre amici che si trovano una sera e decidono di andare insieme a cena in un ristorante della loro città. Alla fine della cena, chiedono naturalmente il conto al cameriere, che immediamente porta loro un biglietto dal quale risulta che la spesa complessiva ammonta a 30000 lire (i prezzi ovviamente si riferiscono a qualche anno fa). A questo punto i tre amici estraggono ognuno una banconota da 10000 lire e la porgono al cameriere, lamentanosi però perchè trovano il conto piuttosto caro, e chiedono quindi al cameriere di andare dal suo capo per chiedere un piccolo sconto. Il cameriere si reca allora dal direttore riferendo quanto gli è stato detto, e quest'ultimo decide di accettare la richiesta applicando uno sconto di 5000 lire. Subito dopo il cameriere prende 5 pezzi da 1000 lire dalla cassa e li riporta ai tre amici, i quali decidono di riprendere 1000 lire a testa e lasciano le restanti 2000 al cameriere come mancia, in segno della sua disponibilità. Usciti dal locale i tre amici cominciano a fare i conti: dunque, ognuno di loro ha in pratica speso 9000 lire, per un totale di 27000 lire, più le 2000 date al cameriere si arriva ad una somma di 29000, ma dove sono finite le restanti 1000 lire che mancano alle 30000 iniziali?

Le noci di cocco

a) Tre marinai trovano un mucchio di noci di cocco. Il primo ne prende la metà più mezza noce. Il secondo prende metà di quello che è rimasto più mezza noce. Anche il terzo prende metà del rimanente più mezza noce. Rimane esattamente una noce che essi danno alla scimmia. Quante erano inizialmente le noci del mucchio? b) Cinque uomini ed una scimmia fecero naufragio su un'isola deserta e passarono il primo giorno a raccogliere noci di cocco per cibo. Poi le ammucchiarono tutte insieme e andarono a dormire. Ma mentre tutti dormivano uno di essi si svegliò e pensando che il mattino dopo vi sarebbero stati dei litigi alla spartizione, decise di prendersi la sua parte. Perciò divise le noci in cinque mucchi. Rimaneva una noce, che egli dette alla scimmia, poi nascose la sua parte e mise tutto il resto assieme. Subito dopo un secondo uomo si svegliò e fece la stessa cosa. Anch'egli dette una noce residua alla scimmia. Uno dopo l'altro tutti e cinque gli uomini fecero la stessa cosa, ognuno prendendo un quinto del mucchio e dando una noce alla scimmia. Alla mattina divisero le noci ed ognuno ottenne lo stesso numero. Naturalmente ognuno sapeva che mancavano delle noci, ma ognuno era colpevole come gli altri e così nessuno parlò. Quante noci c'erano all'inizio? c) E se gli uomini fossero N?

Lo stato di famiglia

Due vecchi amici matematici si ritrovano dopo molti anni, e discorrono per un po'. Il primo fa: "Allora hai tre figli? E quanti anni hanno?". L'altro risponde: "Considerando le loro età come numeri interi, il loro prodotto è 36, e la somma è il numero civico di questa casa qui davanti". Il primo ci pensa un po' e sbotta: "Beh, non mi hai certo dato dei dati sufficienti!" e il secondo ribatte: "Hai ragione: il maggiore ha gli occhi azzurri". Quali sono le età dei tre figli?

Spionaggio

Una spia cerca di capire la regola che associa parola e controparola d'ordine per l'ingresso in un centro segreto. Si nasconde dietro a un cespuglio ed osserva. Arriva un soldato, bussa al portone e da dentro una voce dice "12", il soldato risponde "6" e gli viene aperto. Poco dopo arriva un altro soldato, bussa e gli viene detto "8", lui risponde "4" ed entra. Un terzo soldato entra, dopo avere risposto "5" alla parola "10". A questo punto, la spia crede di aver capito tutto: si avvicina, bussa, le dicono "4", lui risponde "2" e gli sparano. Come mai? (Ovviamente esistono infinite risposte possibili: a noi interessa quella che si esprime con meno parole).

Tre uomini in fuga

Suona l'allarme nel carcere di Rebibbia: al momento del rientro dei detenuti nelle celle, dopo l'ora d'aria, le guardie carcerarie hanno scoperto che tre pericolosi rapinatori sono evasi. Interviene immediatamente la polizia organizzando l'inseguimento dei fuggitivi nei dintorni e sguinzagliando Rex, veloce e abile pastore tedesco, che subito si getta sulle tracce dei fuggiaschi. Gli evasi hanno mezz'ora di vantaggio sui loro inseguitori, ma indeboliti dalla lunga detenzione procedono penosamente a 4 km/ora; i poliziotti, giovani e allenati, coprono senza sforzo 6 km/ora, mentre il cane corre a 12 km/ora. Rex raggiunge gli evasi e immediatamente si volta e torna dai suoi padroni; quando li ritrova, si volta di nuovo e riprende a inseguire i fuggitivi, effettuando quindi una serie di corse e di dietro-front, finché i poliziotti raggiungono e catturano gli evasi. Quanti chilometri ha percorso Rex a questo punto?

Una corda e tre animali

Immaginate di avere una corda lunga quanto la circonferenza terrestre (cioè all'incirca 40000 km), che si trova distesa lungo l'equatore. Immaginate ora di prendere questa corda, di tagliarla, di aggiungervene un metro e quindi di ridistribuirla attorno all'equatore in modo che abbia una distanza dalla superficie terrestre che rimanga costante lungo tutta la circonferenza. La domanda a cui dovete cercare di rispondere è: quale dei seguenti tre animali può passare di misura nello spazio interposto tra la corda e la superficie: una formica, un gatto o un elefante?

La Gallina

Se una gallina e mezzo fa un uovo e mezzo in un giorno e mezzo, quante uova farà una gallina in sei giorni

Test sulla mentalità

Non c'è trucco ne' inganno. Seguite le istruzioni, rispondete alle domande una alla volta e il più rapidamente possibile! Non procedete fino a quando non avete risposto ad ognuna di esse.

Quanto fa:

1+5
2+4
3+3
4+2

5+1

Ora ripetete nella mente il numero 6 piu' velocemente possibile per 30 volte.

PRESTO!!! PENSATE AD UN ORTAGGIO!

PROFILI

SE HAI PENSATO AD UN PISELLO:
Hai una mentalita' decisamente infantile e/o votata ai doppi sensi. Sei decisamente malizioso. Inoltre fai parte di una ristrettissima minoranza.

SE HAI PENSATO AD UNA CAROTA:
Non ci crederai, ma e' scientificamente provato che 98 persone su 100 risponderanno proprio come te. Se non ci credi fai la prova facendo il test ai tuoi amici (funziona anche a voce).

SE HAI PENSATO AD ALTRO:
Il tuo cervello fa delle associazioni completamente strampalate. Il che vuol dire che potenzialmente o sei un genio schizofrenico o sei un futuro serial killer. In ogni caso ti dedicheranno un film.

Due taniche

Avete a disposizione due taniche inizialmente vuote la cui capacità è rispettivamente di 3 e 5 litri. Avendo a disposizione tutta l'acqua che desiderate, e potendo riempire e vuotare le taniche, oltre che potere trasferire acqua da una all'altra, dovete mettere esattamente 4 litri di acqua dentro la tanica da 5. Come bisogna procedere?

I 4 soldati

Ci sono 4 soldati che dopo una battaglia disastrosa stanno battendo in ritirata. Per scappare al nemico devono attraversare un ponte ma:

• il ponte può reggere soltanto due persone per volta
• è buio, e dato che il ponte è malridotto serve una torcia elettrica per attraversarlo, ma naturalmente i 4 soldati ne hanno una sola
• i soldati dopo la battaglia sono in differenti condizioni fisiche, quindi il soldato A ci mette un minuto a fare un attraversamento del ponte, il B ce ne mette 2, il C ce ne mette 5 ed il D ce ne mette 10
• è chiaro che quando due militari attraversano il ponte insieme con la torcia, gli stessi procederanno alla velocità del più lento dei due
• tanto per fargliela facile, i nostri 4 eroi hanno solo 17 minuti a disposizione per trovarsi tutti e 4 dalla parte opposta del ponte.

E allora... come possono fare a tornare al campo base sani e salvi?

I berretti

Tre esploratori vengono catturati da una tribù africana con l'hobby degli enigmi. Il capo tribù decide di graziarli solo se si dimostrano sufficientemente intelligenti. Mostra loro tre berretti rossi e due berretti bianchi. Poi li benda e pone sulla testa di ognuno un berretto rosso. Una volta sbendati ogni esploratore può vedere il berretto sulla testa degli altri ma non il proprio.
Chiede al primo: "Di che colore è il berretto che hai sulla testa?". Il primo osserva gli altri due e risponde che non lo sa.
Chiede al secondo: "Di che colore è il berretto che hai sulla testa?". Il secondo osserva gli altri due e risponde che non lo sa.
Chiede al terzo: "Di che colore è il berretto che hai sulla testa?". Il terzo risponde esattamente dicendo che il proprio berretto è rosso salvando la vita a tutti e tre.
Come ha fatto a saperlo? (Si supponga che i tre esploratori siano dei logici perfetti, cioè siano in grado di dedurre istantaneamente tutte le conseguenze da un insieme di premesse dato).

Il ciclista

Un ciclista scala una montagna alla media di 20 km/h , e poi, giunto in cima, gira la bicicletta e ridiscende a valle (seguendo la stessa strada) ad una media di 60 km/h. Qual è la media complessiva tenuta dal ciclista, durante tutto il suo viaggio?