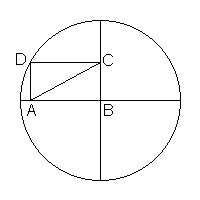
 È immediato notare che la lunghezza di AC vale 1. Infatti la linea AC è
una diagonale del rettangolo e l'altra diagonale BD è evidentemente il raggio
del cerchio che vale 1. Dato che le due diagonali sono uguali, anche AC è lunga
1.
È immediato notare che la lunghezza di AC vale 1. Infatti la linea AC è
una diagonale del rettangolo e l'altra diagonale BD è evidentemente il raggio
del cerchio che vale 1. Dato che le due diagonali sono uguali, anche AC è lunga
1.|
Pagina delle Soluzioni |
L'errore più frequente è di
pensare che se una gallina e mezzo fa un uovo e mezzo in un giorno e mezzo,
allora una gallina farà un uovo in un giorno, invece nò perche al diminuire
delle galline, per fare la stessa quantità di uova ci vuole più tempo.
Ragioniamo quindi nel seguente modo:
se una gallina e mezzo fa un uovo e mezzo in un giorno e mezzo, nello stesso
tempo più galline faranno più uova e quindi
in un giorno e mezzo, 3 galline (2 volte una e mezzo) faranno 2 volte un uovo e
mezzo e quindi 3 uova;
al raddoppiare del tempo, mantenendo constante il numero delle galline
raddoppierà anche il numero di uova fatte e quindi:
in 3 giorni, 3 galline fanno 6 uova;
in 6 giorni, 3 galline fanno 12 uova;
quindi una gallina in 6 giorni fa (12 ÷ 3) uova, cioè 4 uova
Sono sufficiente 3 aerei. I tre aerei A , B e C partono insieme ed arrivati ad 1/8 di giro C trasferisce ad A e B un quarto di serbatoio ciascuno, a C ne rimane un quarto giusto giusto per tornare indietro. Arrivati ad 1/4 di giro B trasferisce ad A un quarto di serbatoio e gliene rimane metà per poter tornare indietro. C , dopo aver fatto il pieno , torna nel senso opposto del giro verso A. Quando A arriva a 3/4 di giro C gli trasferisce un quarto di serbatoio, contemporaneamente parte B raggiungendo A e C esattamente a 7/8 del giro. Dà a ciascuno dei due un quarto di serbatoio e arrivano tutti e tre all'isola in riserva sparata ma sani e salvi.
Il primo esploratore non sa rispondere di che colore è il proprio berretto
perciò evidentemente vuol dire che gli altri due non hanno entrambi il berretto
bianco, altrimenti avrebbe saputo rispondere che il proprio era rosso.
Neppure il secondo esploratore sa di che colore è il proprio berretto, ciò
significa che il terzo non può avere il berretto bianco altrimenti lui avrebbe
detto che il suo è rosso (non potendo essere entrambi bianchi).
Di conseguenza il terzo dice che è il proprio è rosso .
a) La risposta è 15 noci. Infatti se alla fine resta una noce (quella che viene data alla scimmia) vuol dire che il terzo marinaio si è trovato davanti ad un mucchio di 3 noci, dal quale ne ha prese 2, ovvero metà del mucchio (cioè una noce e mezza) più mezza noce, lasciandone 1. Analogamente il secondo marinaio avrà avuto a disposizione 7 noci prendendone 4 (3 e mezzo + 1 mezza noce) e lasciandone appunto 3 per il terzo marinaio. Infine, il primo marinaio poteva disporre di un totale di 15 noci, e ne ha prese 8.
b) La risposta è 3121 noci. In realtà in questo caso la risposta non è unica, ma chiaramente una volta nota una soluzione le altre potranno essere ottenute semplicemente sommando o sottraendo una costante che in questo caso vale 56 = 15625. In questo caso 3121 rappresenta il numero minimo di noci di cocco. Per ricavare questo valore è sufficiente risolvere il seguente sistema.
Y = 5 x A + 1
4 x A = 5 x B + 1
4 x B = 5 x C + 1
4 x C = 5 x D + 1
4 x D = 5 x E + 1
4 x E = 5 x F
in cui Y è il numero totale di noci
all'inizio, F è il numero di noci che ciascun uomo riceve al termine della
spartizione, A B C D E sono il numero di noci prese da ciascun marinaio durante
la notte ed infine il +1 indica la noce che viene ogni volta data alla scimmia.
Da notare che tutti questi valori devono essere interi.
Facendo delle semplici sostituzioni di variabili si ottiene:
1024 x Y = 15625 x F + 8404
A questo punto bisogna risolvere questa equazione tenendo presente che i risultati devono essere interi. Si può anche procedere per tentativi, ma ci sono dei metodi matematici precisi che permettono la risoluzione. Ad esempio ci si può ricondurre ad un problema di programmazione lineare intera (si veda un qualunque libro di ricerca operativa), in cui la precedente equazione rappresenta un vincolo e la funzione obiettivo da minimizzare è semplicemente Y, cioè il numero di noci. Così procedendo si ottiene la soluzione preannunciata 3121.
Per una trattazione più approfondita vi consiglio di consulatare il libro "Enigmi e giochi matematici" di Martin Gardner in cui c'è un intero capitolo dedicato a questo enigma.
c) Nel caso generale la soluzione è data da:
Per N dispari:
(1 + N x K) x NN - (N - 1)
Per N pari:
(N - 1 + N x K) x NN - (N - 1)
con K intero.
La risposta è che passano 200 camion ogni ora. L'automobilista viaggia ad una velocità relativa rispetto ai camion di 40 km/h. Perciò in mezz'ora, percorre 20 km, sempre rispetto ai camion. Questo significa che in un tratto di strada lungo 20 km, ci sono 50 camion, e cioè che ogni camion dista dal successiva 400 m (=20km/50). Dunque tra il passaggio di un camion e l'altro, passano 18 secondi (=0,400/80=0,005 ore) pertanto in un'ora ne passano 200 (=3600/18).
A e B attraversano il ponte e B torna indietro (4 min).
C e D attraversano il ponte e A torna indietro (15 min).
A e B attraversano il ponte e sono tutti in salvo (17 min).
La risposta tipica è "sette", perchè la parola "quattro" ha sette lettere. Infatti in tutti i casi la controparola era il numero di lettere che componevano la parola d'ordine. Come già scritto, le risposte possibili sono infinite...
Lo stato di famiglia |
||||||||||||||||||
Le terne di numeri interi il cui prodotto è 36 (con le somme vicino) sono riportate in tabella. Il secondo matematico conosce la somma (vede il numero della casa) ma non sa rispondere. Questo significa che la somma è 13, l'unico numero che appare due volte. La seconda affermazione del primo matematico ci dice che la risposta giusta è 9-2-2, nell'altro caso infatti si avrebbero due gemelli di 6 anni. |
 È immediato notare che la lunghezza di AC vale 1. Infatti la linea AC è
una diagonale del rettangolo e l'altra diagonale BD è evidentemente il raggio
del cerchio che vale 1. Dato che le due diagonali sono uguali, anche AC è lunga
1.
È immediato notare che la lunghezza di AC vale 1. Infatti la linea AC è
una diagonale del rettangolo e l'altra diagonale BD è evidentemente il raggio
del cerchio che vale 1. Dato che le due diagonali sono uguali, anche AC è lunga
1.
La risposta corretta è: 30 km/h. La risposta più frequente che viene data a questo problema è è invece 40 km/h, basata sul fatto che che il ciclista ha percorso esattamente metà del cammino alla velocità (media) di 20 km/h e esattamente l'altra metà alla velocità (media) di 60 km/h; ma ciò nondimeno, la risposta è errata, giacché procedendo in discesa ad una velocità tripla rispetto a quella tenuta in salita il nostro atleta ha pedalato per un tempo triplo alla velocità di 20 km/h rispetto al tempo in cui è andato a 60 km/h. La risposta corretta è dunque data da v = (3 x 20 + 60) / 4 = 30 km/h. Bisogna cioè tenere conto del peso relativo di ciascuna delle medie.
Non è necessario tenere in alcun conto i dietro-front di Rex, semplicemente:
i poliziotti raggiungono gli evasi dopo 1 ora, il (povero) Rex viaggia alla
velocità costante di 12 Km/h per tutto il tempo, quindi Rex copre 12 Km.
Come si calcola il tempo necessario affinché i poliziotti raggiungano gli
evasi: sia t tale tempo, S lo spazio percorso dagli evasi a partire da quando
inizia l'inseguimento, e quindi (S+2) è lo spazio percorso dai poliziotti,
visto che gli evasi sono in vantaggio di mezz'ora e viaggiano a 4 Km/h (-> si
sono avvantaggiati di 2 Km). allora:
S =4t (= spazio percorso dagli evasi dall'inizio dell'inseguimento)
S+2=6t (= spazio percorso dai poliziotti)
da cui:
4t=6t-2 -> t=1 (ore).
Per ottenere il risultato voluto, bisogna innanzitutto riempire la tanica da 5 e quindi trasferirne 3 litri nell'altra. In questo modo saranno rimasti 2 litri in quella da 5. Successivamente si svuota quella da 3 e si trasferiscono i 2 litri precedenti dalla tanica da 5 a quella da 3. A questo punto riempiamo di nuovo quella da 5 e trasferiamo 1 litro in quella da 3 in modo da riempire quest'ultima. Il risultato ottenuto sarà quello di avere 4 litri di acqua nella tanica più grande.
Per la risoluzione generale di problemi come questo
risulta utile rappresentare ogni configurazione del contenuto delle due taniche
con una coppia di numeri (n1, n2) che rappresentano i
litri d'acqua contenuti rispettivamente nei due recipienti. A questo punto
bisogna costruire un grafo, i cui nodi sono appunto costituiti dalle coppie
descritte in precedenza. A partire da ogni nodo bisogna poi costruire i nuovi
nodi che si possono ottenere applicando una delle regole seguenti:
In questo modo, avremo che nel nostro grafo, da ogni
nodo partiranno alcune frecce dirette verso altri nodi, ed il numero di tali
frecce è uguale a quello delle diverse regole che si possono applicare a quella
particolare configurazione. Una volta completata la costruzione di tale grafo,
avendo attenzione di non introdurre nuovi nodi se questi esistono già, ci
resterà soltanto da individuare il percorso che ci porta dalla configurazione
iniziale a quella finale desiderata. Come molti avranno già potuto notare, non
abbiamo fatto altro che costruire il diagramma degli stati di quello che
comunemente viene chiamato un automa a stati finiti. Questo automa è dotato di
due variabili di stato che coincidono con il contenuto delle due taniche, e di
sei ingressi, che non sono altro le regole applicative. In questo caso l'uscita
dell'automa non è molto significativa, infatti coincide praticamente con lo
stato.
Nel nostro caso il percorso da seguire per raggiungere il risultato voluto è il
seguente:
(0,0) - (0,5) - (3,2) - (0,2) - (2,0) - (2,5) - (1,4)
che è il risultato dell'applicazione delle regole: 2 - 6 - 3 - 6 - 2 - 6.
La risposta è: un gatto. Questa risposta è sorprendente, in quanto si è indotti a pensare che allungare una circonferenza così lunga di una percentuale tanto insignificante provochi un aumento del raggio altrettanto insignificante. Invece questo non è vero, poichè l'incremento subito dal raggio dipende solo dalla lunghezza del pezzo di corda aggiunto e non dal raggio della circonferenza iniziale. Detto questo, il calcolo è veramente immediato. Infatti, indicando con R il raggio terrestre, con PI la costante pi greco e con C=2*PI*R la circonferenza, si ha che la distanza tra la corda e la superficie terrestre vale: d = (C+1)/(2*PI) - R = 1/(2*PI) che vale circa 16 centimetri, e quindi ci può passare sotto un gatto.
Le 1000 lire non sono finite da nessuna parte. Infatti il gioco è intenzionalmente posto con lo scopo di ingannare colui che deve risolverlo. La spiegazione è molto semplice: si può facilmente osservare che le 27000 complessivamente sborsate dai tre amici, sono state così suddivise: 25000 lire al direttore del ristorante e le restanti 2000 sono la mancia data al cameriere.