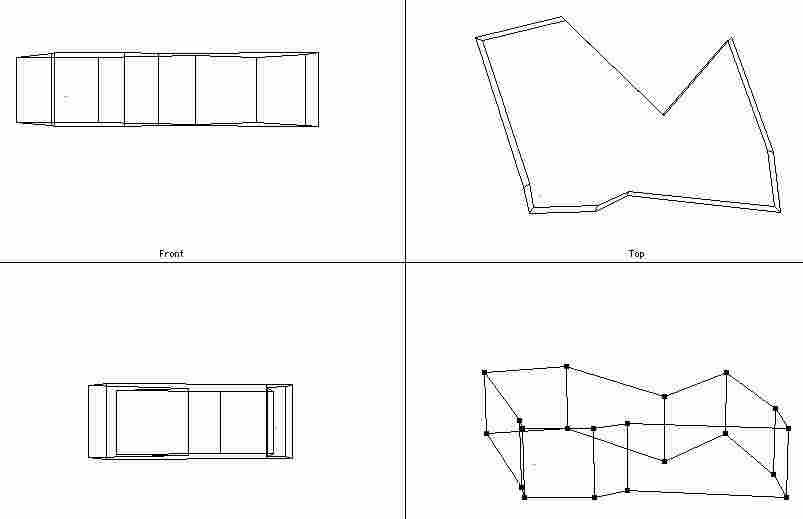
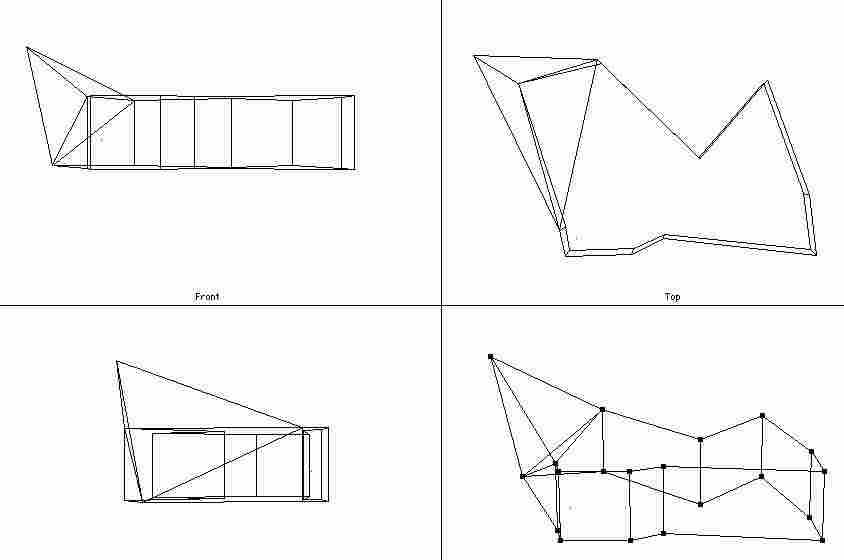
06/05/2002
 
 
Leonardo (4)
 
Lex
 

CUBO

 

PUNTO

 

Famiglia delle ESTRUSIONI 

LINEA

 

Famiglia delle ROTAZIONI 

CERCIO

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

BOULEANE

 

  

Come faccio a trasmettere dei dati tridimenzionali?

Abbiamo già visto il sistema di coordinate; sostanzialmente non esiste differenza nel trattare informazioni di tipo 2d o 3d, dobbiamo però dare delle informazioni di base che aiutino a far capire che tipo di operazione bisogna fare.

Quello che ci serve è un listato delle informazioni che stiamo mandando, come per il 2d, con la differenza che le informazioni descrivono una unità tridimenzionale SHAPE ed il punto di applicazione nello spazio NORMAL del solido.

Ci si muove quindi ad un livello di codificazione superiore di quelli precedenti.

Una volta svelato il meccanismo bisogna:

  •   Capire un formalismo forte per generare    oggetti 3d
  • Capire un sistema inteligente per trasmettere, gestire ed organizzare le informazioni.

 

L'unica cosa che possiamo dire che "esiste" è il punto, anche se è un concetto astratto; esso esiste solo in quanto posizione.

Con un punto (posizione) si possono fare solo dei movimenti che appartengono sostanzialmente a due famiglie:
  • Famiglia delle ESTRUSIONI

Estrusione = movimento che disloca l'oggetto a partire dal suo centro.

Se si estrude un punto si crea una retta e l'oggetto ad una dimensione tramite il movimento acquisisce due dimensioni, estrudendo una retta si ottiene una superficie, ed estrudendo una superficie si avrà un volume; quelli fatti sono tutti movimenti nello spazio di oggetti progressivi, si definiscono così campi che possono essere manipolati come oggetti di livelli crescenti.
Attraverso le estrusioni si possono creare forme molto complesse, ma non si può modificare l'oggetto, non si può rompere la sua natura.
  • Famiglia delle ROTAZIONI

Rotazione = movimento intorno ad un asse, la rivoluzione.

Se si fa ruotare un punto attorno ad un asse si ottiene un cerchio.

Naturalmente esistono numerose variabili in entrambe le famiglie.

Il movimento promuove di un livello

Dal punto si passa alla famiglia delle rette
Dalla retta si passa alla famiglia delle superfici
Dalla superficie si passa alla famiglia dei solidi
Dai solidi si entra in famiglie di complessità crescenti (es: la spazialità)

Se l'unica cosa vera è muovere la posizione del punto, allora qual'è il movimento "magico" costruttivamente, geometricamente, simbologicamente ecc...?
Evidentemente il minimo movimento chiuso, quello che ritorna su se stesso:

IL TRIANGOLO

 

L'altro movimeto decisivo è quello che tende all'infinito, ossia una vera e propria astrazione, un movimento tendente all'infinito di un punto.

IL CERCHIO

 

 

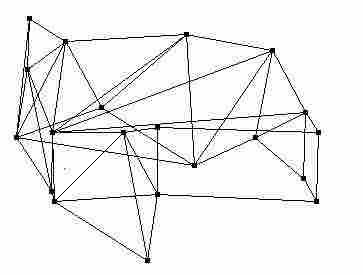
MESH = sistema a rete

Un volume è ridescrivibile con una serie di triangoli, muovendo i punti vivi e creando nuove superfici.

 

 

 

 

Tutto questo appartiene alla famiglia delle SHAPE cioè dei solidi; esiste poi la famiglia delle superfici, che non hanno un interno o un esterno, che sono triangolate ma non chiuse su loro stesse per forza.

 

Sostanzialmente queste famiglie di movimenti si applicano al concetto di movimento, secondo alcune coordinate, di un punto, di una linea o di una superficie.

 

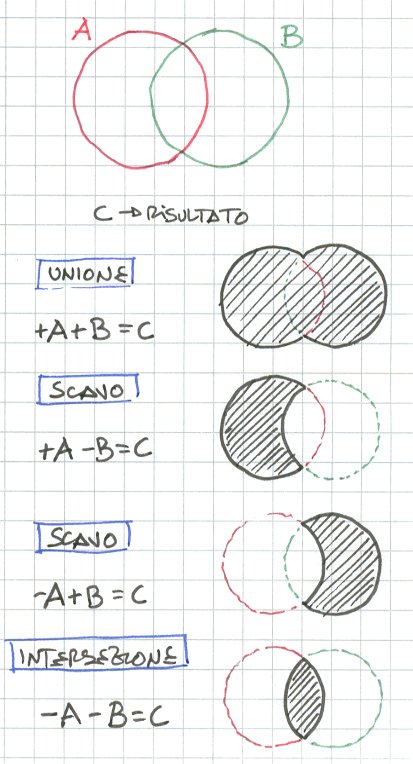
E se invece usassimo un principio associativo di natura logica?

Se abbiamo due entità i rapporti reciproci possono essere un numero matematicamente definito.

Una entità A ed una entità B possono essere, una rispetto all'altra, caratterizzate da un segno geometrico dando vita all'entità C, che sarà il risultato o di una unione, o di uno scavo, o di una intersezione tra le prime due entità.

Queste sono quelle che vengono definite operazioni booleane, utili per creare oggetti più complessi che con le estrusioni e con le rotazioni richiederebbero procedure lunghissime.


 

 

  

 

Torna a: