Vincenzo Calabrò

(Docente di Fisica e Laboratorio presso il Liceo-Ginnasio “B.Russell” di Roma)

v.calabro@iol.it

http://users.libero.it/v.calabro

Una possibile procedura di problem solving di fisica

per studenti di 3° anno di liceo scientifico.

Roma, Marzo 2001

Abstract

“Penso che per dare una mano agli studenti bisognerebbe mettere più impegno nell’inventare problemi che chiariscano i concetti presentati a lezione. Esercizi e problemi forniscono una buona opportunità di completare l’argomento e rendere più reali, più complete, più salde nella mente le idee”.

R. P. Feynmann (Lectures on Physics – 1963)

1. Premessa

Nella prospettiva di apprendere più efficacemente e anche di approfondire le conoscenze di fisica, ho pensato di fare cosa utile agli studenti, desiderosi di apprendere la difficile arte del «problem solving», proponendo loro una possibile traccia di percorso risolutivo di un problema di fisica. Come dice Arnold Arons nel suo bel libro Guida all’insegnamento della fisica [1], risolvere problemi di fisica “è un passo estremamente importante nello sviluppo intellettuale e nella capacità di ragionamento logico astratto degli studenti”. Certo, non è facile risolvere problemi. E’ un’arte difficile, temuta dagli studenti, per cui non è inverosimile che essi vi oppongano resistenza. “La maggior parte degli studenti”, continua Arons, “in questa fase iniziale della loro maturazione, rifiutano di lavorare al problema, o di analizzare le traduzioni da parole a simboli che sono essenziali, fino a che non vedono la soluzione nella sua completezza. Richiedere loro di iniziare comunque la procedura di soluzione li introduce, volenti o nolenti, nel problema, e la spinta così ottenuta spesso li spinge fino alla soluzione. La soddisfazione crescente ottenuta da queste esperienze li rende via via più disponibili a cercare di affrontare un nuovo problema, con carta, penna e metodo, senza aspettare di aver compreso l’intera soluzione”. Arons conclude, affermando che “la grande maggioranza degli studenti inizia a prendere sul serio questo metodo solo se nelle prove di valutazione è richiesto il suo uso e solo se il voto viene abbassato in modo sostanziale nel caso in cui questo metodo non sia usato”. In questa prospettiva pedagogica, non certo facile da gestire, le poche righe che seguono vogliono essere una piccola guida per imparare a risolvere problemi in modo efficace.

2. Per iniziare

Per cominciare, esaminiamo attentamente alcune motivazioni. La fisica è la scienza della natura che studia i fenomeni che avvengono nel nostro universo attraverso il metodo galileiano e in base a leggi fisiche che hanno lo scopo di rendere quantitativi i suoi asserti. Le leggi permettono di costruire delle soluzioni dei fenomeni mediante l’uso di equazioni. Per esempio, un corpo che cade è un fenomeno fisico in quanto evento che si verifica nello spazio-tempo. Bene. Le leggi della caduta affermano che, nel vuoto, l’accelerazione a, la velocità v e lo spostamento x possono essere calcolati secondo le seguenti leggi cinematiche inerenti al moto incipiente:

Se, per esempio, si conoscono l’accelerazione di gravità g e il tempo di caduta t, la soluzione del problema del calcolo dello spostamento x diventa la (3). Se invece si conoscono l’accelerazione di gravità g e la distanza percorsa x, si può calcolare la velocità v attraverso la (4). E’ riduttivo, tuttavia, pensare che le leggi servano solo a costruire soluzioni, benché questo scopo sia uno dei più nobili e importanti della scienza fisica. In realtà esse, in maniera euristica, permettono di scoprire altre leggi e, dunque, altre soluzioni che verranno alla fine inserite in un corpus conoscitivo più organico e completo chiamato teoria. Sono le teorie fisiche, in ultima analisi, lo scopo fondamentale della fisica in grado di produrre conoscenza dei meccanismi di funzionamento del nostro universo.

3. Il metodo

E parliamo di “problem solving” che nella sua accezione corretta significa “metodo di risoluzione” di un problema. In generale il problem solving permette di:

• ricercare la soluzione,

• descrivere la soluzione,

• verificare la soluzione.

La ricerca, la descrizione e la verifica della soluzione di un problema di fisica si può ottenere abbastanza facilmente mediante una specifica metodologia che è valida anche al di fuori della fisica vera e propria. Il problem solving, pertanto, fornisce degli strumenti culturali di tipo scientifico che permettono di ottenere la soluzione di un problema.

Quello che propongo in questa breve presentazione è un possibile modello di problem solving, che con un termine colorito definirei “a cipolla”. La ragione è che questo modello è fatto di ragionamenti a più livelli, a strati, proprio come in una cipolla. Si tratta di una particolare metodologia tra tutte quelle possibili per risolvere, con un certo grado di affidabilità, problemi di fisica. La svilupperò non solo per il ruolo importante che essa riveste all’interno dello studio della fisica e per le ricadute che mostra nell’apprendimento, ma anche perché è una metodologia che fornisce dei concetti chiave e delle procedure razionali che sono validi ben oltre la fisica medesima, in quanto forniscono allo studente strumenti intellettuali di analisi e di sintesi della complessa realtà fisica nella quale egli vive. E, poi, avvia a saper risolvere problemi.  Il che non è poco.

4. Il progetto risolutivo nei suoi sviluppi operativi

Ecco in breve e schematicamente la linea metodologica della ricerca della soluzione di un problema di fisica con il metodo a ”cipolla”. Data la natura procedurale del metodo è necessario comprendere che la base metodologica consiste, almeno all’inizio,  nel capire la necessità di operare sempre a tre livelli. Essi sono:

A.     astrazione sul fenomeno;

B.     astrazione sui dati;

C.     suddivisione e gerarchie.

A) Cominciamo dal primo punto. Cosa significa “astrazione sul fenomeno”? Premesso che risolvere un problema richiede un notevole sforzo e una capacità di invenzione non certo banale è necessario innanzitutto leggere bene, più volte, il testo del problema e comprendere il fenomeno fisico in esame. Astrarre è un verbo che costringe a pensare, riflettere, analizzare ciò che il fenomeno evidenzia. Significa individuare un valore separandolo e isolandolo, con un procedimento mentale, da altri valori conosciuti. Per esempio, se il testo del problema riguarda un oggetto a forma di corona circolare avente  un certo spessore, a mo’ di cilindro bucato, costituito da un determinato materiale di cui si deve determinare la massa, allora astrazione sul fenomeno significa individuare attentamente la forma dell’oggetto, collegandola con la figura geometrica di cui è possibile individuare le formule per il calcolo delle grandezze geometriche interessate alla soluzione (in questo caso la superficie della corona cilindrica forata e il suo volume). Dunque, astrarre è una operazione mentale del pensiero che opera per permettere di identificare nel corpo della scienza i modelli fisico-matematici (nel nostro esempio si tratta di un modello geometrico) a cui si riferisce l’oggetto. Uno schema, un disegno del corpo in esame, anche molto incerto, e un formulario delle grandezze coinvolte  nel fenomeno aiutano a comprendere meglio il fenomeno stesso e rappresentano un momento importante di sintesi e di astrazione dell’attività di problem solving.

B) Il secondo punto riguarda l’”astrazione sui dati”. Astrarre sui dati significa farsi delle idee sugli aspetti quantitativi (proprietà) dell’oggetto, cioè significa avere chiaro il gruppo di grandezze fisiche coinvolte di cui si conoscono le misure. Vuole dire, in altre parole, identificare con precisione non solo quali sono le informazioni conosciute ma anche quelle da determinare, cioè le incognite. In più, dà un’idea dell’ordine di grandezza di ciò che si deve calcolare.

Le astrazioni sul fenomeno e  sui dati, in conclusione, vogliono dire identificare alcune proprietà fisiche importanti del fenomeno e indirizzare la nostra concentrazione mentale solo su queste ignorando le altre. Le leggi della fisica forniscono allo studente strumenti di indagine per realizzare un modello astratto in modo tale da avere chiaro in mente cosa è rilevante da ciò che non lo è.

C) Al terzo e ultimo punto vi è la questione della suddivisione e delle gerarchie. “Dividere” un problema significa ripartire in livelli come in una cipolla che è costituita da strati e attraverso questa operazione astrarre aspetti importanti del problema. “Gerarchizzare” i livelli significa individuare una precisa gerarchia, un ordine, nel senso di livelli che vengono prima da livelli che vengono dopo, così come in una cipolla ci sono strati più interni che sono “sotto” e strati più esterni che sono “sopra”. Inoltre, l’astrazione deve permettere di emarginare alcuni dettagli del fenomeno in modo tale da permettere di concentrarci solo su alcuni aspetti che fanno parte del problema. Quindi, risolvere un problema ha a che vedere con una divisione di compiti. E’ altresì importante comprendere che il problema lo si deve suddividere in sottoproblemi più semplici perché, in generale, si risolvono bene solo i piccoli problemi. Cioè, si risolvono bene i problemi per i quali già si conosce la soluzione. Per esempio, gli esemplari di Kuhn [9] sono  concrete soluzioni di semplici problemi che si incontrano all’inizio della educazione scientifica. Oppure, che siano diversificazioni di un problema noto o di quelli per i quali si vede subito una soluzione. I romani nell’antichità dicevano divide et impera, cioè un problema complesso è meglio suddividerlo in tanti piccoli problemi. Si trovano, quindi, le soluzioni di ogni frammento in modo separato, come in un puzzle, e poi si rimettono insieme le parti. Naturalmente la suddivisione di un problema complesso in tanti piccoli sottoproblemi è un’operazione non facile. Non esiste una tecnica stabilita una volta per tutte che ci insegna a suddividere il problema in tanti sottoproblemi. Quello che sappiamo è che è utile dividere, perché ottenere sottoproblemi più semplici, ragionevolmente indipendenti, che siano ciascuno risolubili per conto proprio in modo indipendente dagli altri, è la migliore delle tecniche possibili per ottenere la soluzione dell’intero problema di fisica.

5. Quadro riassuntivo

L’elenco dei consigli che posso proporre a questo punto può essere il seguente.

• Leggere attentamente e comprendere il testo del problema.

• Preparare un elenco completo delle grandezze fisiche note e di quelle da determinare (incognite)

• Disegnare uno schema del fenomeno. Nei problemi che prevedono grandezze vettoriali, assicurarsi di avere disegnato tutti i vettori (spostamenti, velocità, forze, ecc.). In particolare disegnare sempre le forze che agiscono su un dato corpo o punto materiale (diagramma delle forze). L’analisi delle forze può aiutare ad organizzare mentalmente i dati e può suggerire utili equazioni risolutive del problema.

• Altro suggerimento utile è quello di scrivere nelle equazioni i simboli delle grandezze fisiche complete delle informazioni specifiche, come nel caso di scrivere v_f e v_i o v₂ e v₁ per indicare la velocità finale e iniziale di un corpo in movimento.

• Scrivere le equazioni completamente in simboli prima di inserire nella formula i valori numerici.

• Individuare le condizioni e le leggi fisiche inerenti al fenomeno in esame, spezzettando il problema in più sottoproblemi più semplici mediante

• l’analisi delle relazioni matematiche che sono valide nelle condizioni date. Assicurarsi sempre che tali relazioni siano applicabili al caso in esame. E’ molto importante sapere quali sono le limitazioni di validità di ogni relazione o formula (per esempio non è possibile accettare per la massa di un corpo un valore negativo).

• Molte volte le incognite sembrano in numero troppo elevato rispetto al numero di equazioni individuate. In tal caso è bene chiedersi, ad esempio, se esistono altre relazioni matematiche ricavabili dalle condizioni del problema e/o se è possibile combinare qualcuna di queste equazioni per eliminare alcune incognite.

• E’ buona norma risolvere tutte le equazioni algebricamente in termini letterali e sostituire i valori numerici solo alla fine. E’ necessario scrivere sempre le unità di misura, poiché questo può servire come controllo.

• Accertare se la soluzione trovata è dimensionalmente corretta.

• Arrotondare il risultato finale allo stesso numero di cifre significative che compaiono nei dati del problema.

•  Ricordare che per imparare a risolvere bene i problemi è necessario risolverne molti: il problem solving richiede frequentemente creatività, ma è possibile che con l’abitudine si riuscirà a risolvere un problema partendo da un altro già risolto.

6. Esemplificazione

Possiamo vedere adesso, in modo schematico, un semplice e istruttivo esempio di tecnica di gerarchia di livelli applicata al calcolo della massa m di una corona circolare cilindrica di raggi r₁ e r₂, con densità d e spessore x. Cominciamo a individuare dati, incognite ed equazioni del fenomeno:

Dividiamo successivamente il problema in una gerarchia di tre sottoproblemi semplici e vedremo che la soluzione diventa facile. Ecco il risultato della suddivisione del problema in tre sottoproblemi:

SP: massa= V d         SP: volume=S x         SP: superficie= π r²

Quale dei tre sottoproblemi risolvere per primo? Ogni sottoproblema è indipendente da quello successivo ma dipende da quello precedente perché ogni sottoproblema inferiore fornisce il dato mancante al sottoproblema superiore, come in una catena unidirezionale in cui il precedente è indispensabile al conseguente. Infatti per calcolare il volume è necessario conoscere la superficie, mentre per calcolare la massa è vincolante conoscere il volume e, quindi, la superficie. Si crea pertanto una gerarchia di strato che nel nostro caso assume la seguente successione:

SP1  à   SP2  à   SP3

La gerarchizzazione dei sottoproblemi ci informa che, pertanto, è la superficie la grandezza fisica che è necessario calcolare per prima. Pertanto iniziamo da essa.

·        Sottoproblema1 – Calcolo della superficie della corona circolare: 

(5)        S=S₂-S₁=π r₂²- π r₁² = π (r₂²- r₁²).

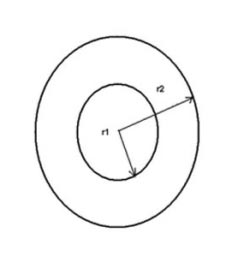
Non è importante calcolare il valore numerico della superficie. Non serve. Il problema non ce lo chiede. E sarebbe anche una fatica sprecata e una perdita di tempo. Non facciamo cose  non  richieste. Lasciamo la formula così come l’abbiamo scritta.

Calcolata la superficie è possibile risolvere il secondo sottoproblema. Sia chiaro che ciò è possibile perché prima abbiamo risolto il sottoproblema1. Senza quest’ultimo non sarebbe stato possibile risolvere il secondo. Dunque, gerarchizzare significa che per calcolare il volume era necessario disporre della formula della superficie che è a un livello più basso del volume.

·        Sottoproblema2 – Calcolo del volume della corona circolare: 

(6)       V=S x= π (r₂²- r₁²) x.

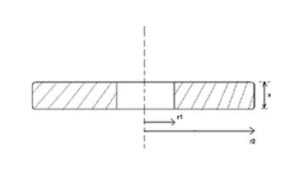
Anche qui, lasciamo la sola formula. E’ inutile calcolare il valore numerico del volume. Non serve. Nessuno ce lo ha chiesto. Infine, risolviamo il terzo e  ultimo sottoproblema, che nel nostro caso coincide con la soluzione del problema stesso.

·        Sottoproblema3 – Calcolo della massa della corona circolare: 

(7)       m=V ∙ d.

Sintetizziamo, adesso, il tutto con la formula risolutiva:

Ora, e solo ora, si può procedere al calcolo della massa, sostituendo ai simboli i valori numerici. Il risultato sarà un numero, chiamato misura della massa, con una unità di misura che, se si sono utilizzate le unità di misura del S.I., è il kg.

7. Un nuovo problema

Risolviamo adesso un problema meno banale di quello proposto sopra. Si tratta di un problema di meccanica, in particolare di un problema che viene generalmente dato agli studenti quando si studia il lavoro e l’energia meccanica. Il problema si trova a pag. 144 del 1° volume del manuale di fisica D.Halliday-R.Resnick-J.Walker, Fondamenti di fisica. Meccanica, Bologna, Zanichelli, 2001. E’ il «numero 26P» presente a pag.144, il cui testo è il seguente:

Ricerchiamo insieme la soluzione. Prima però diciamo che il metodo “a cipolla” verrà qui applicato in maniera sintetica, senza cioè seguire pedantemente la traccia di lavoro proposta in precedenza. Non è possibile a questi livelli rimanere legati a uno schema troppo rigido che prevede interventi troppo schematici che limiterebbero il lavoro di ricerca della soluzione. Il metodo, tuttavia, rimane inalterato e applicabile sempre in qualunque circostanza.

Il problema si propone l’obiettivo di calcolare il lavoro svolto dalle tre forze Ti (i=1,2,3) esercitate in successione dall’argano sullo speleologo lungo i tre tratti di uguale percorso di lunghezza x.

Partiamo subito da una premessa fisica molto importante. Esistono due oggetti meccanici che interagiscono fra loro. Essi sono l’argano che produce delle forze e lo speleologo che le subisce. Dunque, dal punto di vista terminologico e concettuale, ricorderemo sempre nel seguito, anche a costo di essere ridondanti, che uno dei due oggetti (l’argano) è la causa della tipologia di moto subita dall’oggetto perché produce delle forze che agiscono sull’altro (lo speleologo) il quale, poveretto, è costretto a subire gli effetti delle cause, cioè è costretto a subire delle accelerazioni più o meno intense perché prodotte dalle forze ad esso applicate. Si tratta, pertanto, di un ideale problema di meccanica classica nel quale entrano in gioco delle forze che producono lavoro.

Dal punto di vista generale il problema non presenta grosse difficoltà. Si tratta infatti di costruire un modello dinamico di forze applicate al corpo in grado di determinare le tre forze risultanti costanti T₁, T₂ e T₃ con le quali si possono calcolare (in joule)  i tre lavori incogniti L₁, L₂ ed L₃ compiuti. Il modello è rappresentato da un insieme di vettori che modellizzano il fenomeno, nel senso che riescono a produrre una rappresentazione astratta della realtà fisica costituita da operatori matematici in grado di rappresentare quantitativamente il fenomeno in esame. La formula di definizione del lavoro nei tre casi  è sempre la stessa ed è quella relativa al lavoro prodotto da una forza T che sposta il proprio punto di applicazione di una distanza x. In formula:

(9)     L_i = T_i  ∙ x = T_i x cosθ

Qui cosθ rappresenta il coseno dell’angolo esistente tra i due vettori forza e spostamento. Dal punto di vista specifico il problema presenta un doppio ostacolo. Il primo consiste nel dover calcolare innanzitutto le accelerazioni a_i subite dallo speleologo nel mentre viene sollevato verso l’alto dall’argano lungo i tre spostamenti x. Il secondo ostacolo consiste nel dover calcolare, anche qui in via preliminare, i moduli delle tre forze T₁, T₂, T₃ che permettono alla fine di determinare i rispettivi tre lavori secondo la (9). Cominciamo dalla prima questione, dicendo subito che l’accelerazione dello speleologo sarà diversa nei tre casi. Esaminiamoli separatamente e commentiamoli con ponderazione. Prima però proponiamo la soluzione completa posta in forma sintetica. Eccola.

Stadio 1)

Lo speleologo, qui inteso come punto materiale di massa m=80 kg, parte da fermo (velocità v_o= 0) e nel tratto di lunghezza x=10 m accelera in modo tale da raggiungere gradualmente e costantemente la velocità finale v=5 m/s nel momento in cui ha percorso l’intero primo stadio di 10 m. E’ evidente che è necessario calcolare questo valore costante dell’accelerazione, che chiameremo a₁, senza il quale è impossibile calcolare il valore, anch’esso costante, della forza T₁ esercitata dall’argano sullo speleologo durante il sollevamento nei primi 10 m e necessario a imprimergli la velocità finale di 5 m/s. Quali sono le grandezze fisiche interessate al fenomeno del sollevamento dello speleologo dal fondo della cavità all’altezza dei primi 10 m di percorso? E, soprattutto, quale formula lega le grandezze fisiche in gioco durante questo primo segmento di moto? Le grandezze cinematiche interessate al moto sono cinque: la distanza percorsa x, la velocità iniziale v_o, la velocità finale v (che sono dati), l’accelerazione a₁ e il tempo t impiegato (incognita) per coprire lo spostamento subito dallo speleologo. Aggiungiamo che anche le forze e i lavori sono incognite. Chiarito subito che la velocità iniziale v_o è zero perché il corpo parte dal fondo del pozzo da fermo, le quattro grandezze rimanenti t, x, v ed a sono legate tra di loro da espressioni algebriche rappresentate dalle normali leggi cinematiche del moto vario ad accelerazione costante x=x(t), v=v(t) e a=a(t). Nel nostro caso diventano: x=½a∙t², v=a∙t, a=costante. Osservazione importante sembra essere quella che è necessario fissare preventivamente una direzione positiva dell’asse verticale (y) verso l’alto. Ci servirà per determinare il segno dell’accelerazione. Inoltre, lo diciamo come premessa, l’analisi fisica del modello di moto dello speleologo prevede che esso si muova in assenza di resistenza del mezzo, cioè nel vuoto e il sistema di riferimento si immagina fissato con il terreno dal quale lo speleologo si allontana nel momento in cui inizia il proprio moto ascensionale verso l’alto. L’accelerazione dello speleologo, causata dal sollevamento prodotto dall’argano, è positiva (e dunque >0) nel primo tratto di 10 m a causa del fatto che la sua velocità cresce da 0 a 5 m/s. In realtà la ragione ultima è che essa è positiva perché è positiva la forza risultante R₁ di sollevamento prodotta dall’argano (a₁=R₁/m). E R₁ è positiva perché essa agisce lungo lo stesso verso positivo dell’asse verticale y delle ordinate. Il calcolo del modulo di a₁ porta a un valore di +1.25 m/s². A questo punto è possibile determinare il modulo della forza T₁ prodotta dall’argano sullo speleologo lungo il primo stadio x=10 m. Questa forza costante risulta composta di due parti. La si può calcolare mediante l’utilizzo del diagramma di tutte le forze applicate allo speleologo. Su quest’ultimo, infatti, agisce una forza risultante T₁-mg, dovuta al fatto che la forza dell’argano è positiva verso l’alto e la forza peso è negativa perché diretta verso il basso. Il peso dello speleologo, com’è noto, è uguale al prodotto della massa gravitazionale dello speleologo per l’accelerazione di gravità g locale nel punto in cui si trova lo speleologo. La forza risultante T₁-m∙g, per il 2° principio della dinamica, produce una accelerazione a₁ il cui modulo è uguale al prodotto della sua massa inerziale m per la sua accelerazione a₁. Dunque:

(10)   T₁-m∙g=m∙a₁.

Portando il termine m∙g al secondo membro si ottiene:

(11)   T₁=m∙g+m∙a₁ .

Il primo termine m∙g del secondo membro della (11) serve per annullare il peso del corpo dello speleologo, mentre il secondo termine m∙a₁ serve per imprimere allo stesso l’accelerazione a₁ necessaria per aumentare linearmente la sua velocità da 0 a 5 m/s come detto dal testo del problema. E’ evidente che la forza totale esercitata dall’argano è la somma dei due termini, cioè:

(12)   T₁=784 N + 100 N = 884N.

E’ rilevante far notare che nella (12) solo 1/9 circa della forza totale produce l’accelerazione a₁ subita dallo speleologo nella prima parte del suo tragitto, mentre i rimanenti 8/9 servono esclusivamente ad annullare l’azione del peso

(13)      p=m∙g

dello speleologo prodotto dalla Terra.

Stadio 2)

Lo speleologo, all’inizio del secondo stadio, possiede adesso una velocità iniziale di 5 m/s che viene mantenuta costante per l’intero spostamento verticale x. Ciò può essere realizzato, in sintonia con il 1° principio della dinamica, nella condizione fisica di applicare una forza costante esterna T₂ verso l’alto prodotta dall’argano uguale e contraria alla forza peso costante (13) esercitata dalla Terra sulla massa gravitazionale m dello speleologo in modo tale che la risultante delle due forze applicate allo speleologo R₂=T₂-m∙g è nulla. In altre parole, vista la costanza della velocità v=5 m/s, la forza risultante R₂ deve essere zero. Peraltro, questa forza T₂ risulta inferiore a quella precedente T₁ per il semplice fatto che essa non deve aggiungere al moto ascensionale dello speleologo la parte di moto dovuta all’accelerazione del corpo, come nel primo caso. Basterà pertanto che sia:

(14)  T₂=m∙g=784 N

e il gioco è fatto. Questa forza applicata allo speleologo ha l’effetto di annullare l’azione gravitazionale della Terra (13) realizzando un moto rettilineo uniforme verso l’alto a causa dell’assenza sia di una risultante R₂≠0 e sia di forze non conservative di attrito del mezzo. Infatti, la risultante delle forze applicate sullo speleologo è:

(15)   R₂=∑T_i=+T₂ - m∙g=784 N-784 N=0.

Il corpo dello speleologo, di massa inerziale m=80 kg, si muoverà in modo uniforme senza scosse a velocità costante e senza variazione di moto (∆v=0) percorrendo la distanza

(16)       x=v∙t

nel tempo t a velocità costante v.

Stadio 3)

Nel terzo e ultimo stadio, sempre di lunghezza x=10m, lo speleologo sarà sottoposto a una forza risultante

(17)       R₃=-m∙g+T₃

 verso il basso uguale al valore assoluto della differenza tra la sua forza peso mg rivolta verso la direzione negativa dell’asse y e l’azione dell’argano verso l’alto T₃, il cui valore minore di m∙g impone allo speleologo di diminuire la propria velocità da 5 m/s a 0 con un ∆v<0. Dunque:

(18)       T₃=m∙g - m∙a=784 N-100 N=684 N .

Da notare che questa volta la forza mg verso il basso (peso del corpo) è maggiore di quella T₃ verso l’alto (forza di sollevamento dell’argano). Dunque, la risultante delle forze è R₃<0 e la relativa accelerazione a₃ sarà anch’essa negativa (a₃<0). L’argano, in quest’ultimo tratto, “recupera” i 1000 J (prodotti dalla forza di 100 N per spostare il suo punto di applicazione di 10 m) che aveva “perduto” nel primo stadio quando era stato costretto a imprimere allo speleologo l’accelerazione positiva a₁=+1.25 m/s². Adesso l’accelerazione posseduta è a₃=-1.25 m/s². Questo fatto impone al corpo di diminuire la sua velocità da 5 m/s a 0 (∆v<0).

E’ interessante far notare che i tre lavori L₁, L₂ ed L₃ ancora da determinare, peraltro tutti positivi perché lavoro motore, sono diversi, come d’altronde sono diverse le tre forze che agiscono sullo speleologo durante il sollevamento per produrre il lavoro. Questo fatto è evidente vista la natura del moto nei tre tratti. Questi segmenti di  moto sono:

1. nel primo stadio costantemente accelerato (a>0)
2. nel secondo stadio sempre uniforme (a=0)
3. nel terzo stadio costantemente decelerato (a<0).

E’ ovvio che se si desidera accelerare un oggetto tirato verso l’alto come nel primo tratto è necessario applicare una forza T₁ maggiore di quella T₂ che permette all’oggetto di muoversi a velocità costante. Se poi il moto è addirittura decelerato, nel senso che inizialmente la velocità ha un valore di 5 m/s e alla fine questa velocità si annulla, la forza T₃ applicata sarà di intensità ancora minore che non nei casi precedenti. Per realizzare quest’ultimo tipo di movimento, che è un moto rettilineo uniformemente ritardato, con accelerazione negativa e velocità decrescente da 5 m/s a 0, la forza T₃ dovrà essere minore dei valori precedenti: T₃ < T₂ < T₁. A noi risulta T₃= +100 N, T₂=0 e T₃= -100 N.

I tempi  di percorrenza

Lo speleologo viene sollevato dall’argano per tre successivi percorsi uguali di 10 m. Ci chiediamo quali sono i tempi impiegati per coprire le varie distanze.

1)      Il primo tratto di percorso x₁ si può ottenere con l’equazione del moto x₁=½ a∙t₁² da cui

(19)     t₁=√(2x₁/a₁)=√(2 ∙10/1.25)=4 s 

2)      Il secondo tratto x₂=v∙t₂ da cui

(20)     t₂=x₂/v=10/5=2 s

3)      Il terzo tratto   

(21)         x₃=v∙t₃-½a∙t₃²

che è un’equazione di 2° grado nell’incognita t₃. Pertanto l’equazione diventa

10=5 t₃-0.625 t₂² ,

cioè  

0.625 t₃²-5 t₃+10=0

e, infine,      

(22)   t₃=[5±√(5²-25)]/1,25=±4 s

dove la soluzione t₃=-4 s deve essere scartata.

In conclusione, lo speleologo percorrerà i tre tratti uguali del percorso, rispettivamente in 4 s con moto uniformemente accelerato, in 2 s con moto uniforme e di nuovo in 4 s con moto uniformemente decelerato.

I diagrammi orari

Tracciamo adesso i grafici delle tre grandezze fisiche x(t), v(t) ed a(t) in funzione del tempo. Per primo disegniamo il diagramma orario (Fig.1) di come varia la posizione x in funzione del tempo t.

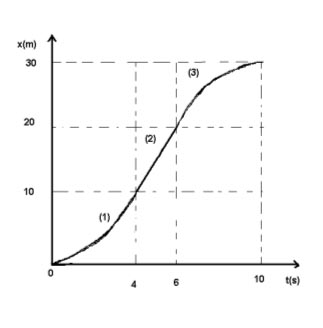
Fig.1 – Diagramma orario x=x(t) del moto dello speleologo

Lungo il tratto (1) si ha un tratto di parabola con la concavità verso l’alto perché l’accelerazione a₁ è >0. L’equazione del moto generale

x=xo+vo ∙ t+½ a∙t²

diventa:

x₁(t)=½ a₁∙ t²

dove a₁ è l’accelerazione a₁=+1.25 m/s².

Lungo il tratto (2) si ha una retta con pendenza costante. L’equazione generale del moto è

x=x₀+v∙t

Diventa nel nostro caso

x₂=v∙t

Dove v è la velocità costante di 5 m/s impressa allo speleologo dall’argano alla fine del primo tratto. Chiaramente, l’accelerazione a₂ durante questo percorso, è zero perché il moto ha velocità costante.

Lungo il tratto (3) si ha un ramo di parabola con la convessità verso l’alto. Il moto è decelerato perché a<0. Dall’equazione generale

x=xo+vo ∙ t+½ a∙t²

si ha

x₃=vo ∙ t-½ a∙t²

dove a₃ è l’accelerazione a₃= -1.25 m/s².

In secondo luogo disegniamo il diagramma orario (Fig.2) di come varia la velocità v in funzione del tempo t.

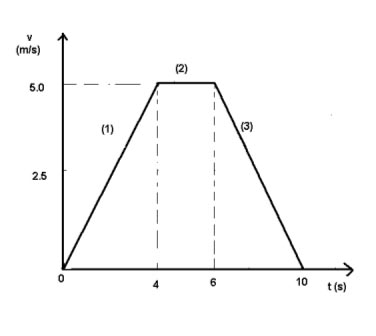
Fig.2 - Diagramma  v=v(t) del moto dello speleologo

Anche qui il tratto (1) è un tratto di retta con pendenza positiva dovuto al moto rettilineo uniformemente accelerato che aumenta linearmente la velocità dello speleologo da 0 a 5 m/s.

Nel secondo tratto (2) il diagramma mostra un tratto di retta orizzontale, parallela all’asse dei tempi, con pendenza nulla dovuto al moto prodotto dall’assenza di una risultante delle forze diversa da zero.

Il terzo e ultimo tratto (3) è un tratto di retta con pendenza negativa dovuto al moto rettilineo uniformemente ritardato subito dallo speleologo che diminuisce la sua velocità dal valore iniziale di 5 m/s al valore 0.

Infine, disegniamo il diagramma orario (Fig.3) di come varia l’accelerazione a in funzione del tempo t.

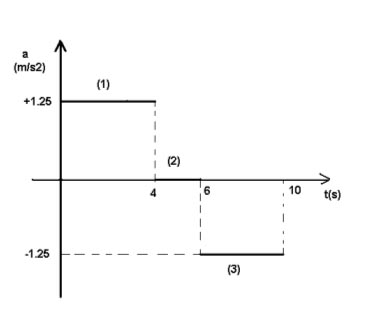
Fig.3 - Diagramma  a=a(t) del moto dello speleologo

In quest’ultimo caso si hanno tre tratti di grafico costituiti da segmenti orizzontali paralleli all’asse dei tempi in cui l’accelerazione è sempre costante ma assume valori diversi. La differenza sta nel fatto che nel primo tratto (1) l’accelerazione è positiva (a>0), nel secondo tratto è zero (a=0) e nell’ultimo tratto è negativa (a<0).

Il lavoro nei tre stadi effettuato dall’argano sarà:

Un metodo alternativo.

 Esiste un’altra maniera per risolvere il problema. Il nuovo metodo è concettualmente interessante e merita di essere indicato perché sfrutta il teorema “lavoro-variazione di energia cinetica”, cioè: L=ΔK. Vediamo in cosa consiste. Se indichiamo con L_o il lavoro compiuto dall’argano per sollevare lo speleologo a velocità costante questo lavoro sarà: L_o=m·g·x. Esso sarà uguale per tutti e tre gli stadi di trascinamento. Il valore numerico di questa base comune di lavoro è: L_o=80·9.8·10=7840 J. Adesso prendiamo in considerazione singolarmente i tre stadi e consideriamo le variazioni di energia cinetica che interessano lo speleologo. Nel primo stadio l’argano imprime una accelerazione positiva +a con una forza aggiuntiva F_a=m·a al valore base. Questa forza aggiuntiva produce un lavoro aggiuntivo L_a che va ad aumentare l’energia cinetica dello speleologo secondo la relazione L_a=K_f-K_i=½m·v² - ½m·v_o² = ½80·5² - 0=+1000 J. Questo lavoro deve essere aggiunto a quello precedente perché, come abbiamo già detto, va ad aumentare l’energia cinetica dello speleologo aumentandone la velocità durante la fase di accelerazione. Dunque: L₁=L_o+L_a=7840+1000=8840 J. Nella seconda fase il teorema L=ΔK ci dice che essendo la velocità costante non interviene alcuna modifica dell’energia cinetica dello speleologo. Dunque, il lavoro aggiuntivo è nullo e il lavoro compiuto in questa seconda fase rimane lo stesso di quello base: L₂=L_o=7840 J. Nell’ultima fase, al contrario, il moto è decelerato (a<0), l’argano è costretto a imprime una accelerazione negativa -a prodotta da una forza negativa F_a=-m·a. Questa forza produce un lavoro aggiuntivo negativo -L_a che va a diminuire l’energia cinetica dello speleologo secondo la relazione: L_a=½m·v_o² - ½m·v² = 0 - ½ 80·5² = -1000 J. Il lavoro nella terza fase sarà pertanto: L₃= L_o-L_a= 7840-1000 = 6840 J. Come si può vedere i risultati coincidono con quelli ottenuti precedentemente. 

Il problema è stato risolto. Abbiamo calcolato i tre lavori prodotti dall’argano durante i tre stadi del sollevamento dello speleologo. E’ evidente che il fenomeno fisico in esame non si presenta nella realtà così come proposto dal testo. In altre parole, non si avranno mai situazioni di discontinuità brusche e improvvise come quelle rilevate nei grafici in cui si passa istantaneamente, per esempio, da un valore dell’accelerazione positiva a un’altra nulla o negativa o da valori della velocità uniformemente crescenti a valori improvvisamente costanti. In realtà i cambiamenti in natura saranno continui e mai sottoforma di netta e fulminea singolarità. Ci si potrà chiedere pertanto perché abbiamo discusso parecchio su situazioni apparentemente irrealistiche. Una prima risposta potrebbe essere che lo abbiamo fatto perché l’analisi fisica del fenomeno del sollevamento è stata enormemente semplificata proprio da questa scelta. Galileo quando analizzò il moto di caduta di un grave non scelse il moto complicato di una foglia che cade all’interno di una massa d’acqua in una cascata. Al contrario, semplificò il fenomeno per rendere il modello matematico facilmente trattabile. Una seconda risposta è che le analisi di situazioni coinvolgenti cambiamenti bruschi e discontinui si avvicinano a una quantità notevole di casi reali con buona approssimazione. Ma dal punto di vista didattico la risposta più significativa che si può dare è che nell’apprendimento della fisica è tremendamente importante imparare ad avvalersi del metodo. Da questo punto di vista la dimensione metodologica dell’analisi fisica dei fenomeni naturali, e conseguentemente il problem solving, sono gli obiettivi più importante che un docente di fisica si pone nel progettare il suo insegnamento.

8. Conclusioni

Il metodo “a cipolla” è un buon metodo per iniziare a risolvere problemi di fisica. Costringe a ragionare, sviluppa una logica operazionale e dà una traccia precisa per ricercare la soluzione. Naturalmente è necessario non essere meccanici e ripetitivi nella applicazione concreta del metodo. Come in tutte le cose che prevedono una comprensione metodologica è necessario avere una certa fantasia e una certa elasticità mentale, ed è importante che lo studente si appropri del metodo, lo utilizzi criticamente, più volte, per abituarsi a ragionare. E’ evidente che alcuni problemi possono risultare di difficile risoluzione. Non ci si deve meravigliare se il metodo non dà subito i risultati voluti. Si tenga conto che, come dice G.Cavaggioni nell’utile libro Le Olimpiadi della Fisica [6], “anche gli insuccessi che seguono a un attento impegno possono essere utili a sviluppare le capacità di analisi e di comprensione dei concetti della fisica più che un precoce ricorso a soluzioni proposte da altri”. Dunque, ancora una volta è valida la massima che  afferma: “sbagliando si impara”.

Ricordo, in conclusione, che nessun metodo, buono per quanto possa essere, può dare risultati concreti se non si studia adeguatamente e con continuità. Dunque, alcune volte, piuttosto che affrettarsi a leggere il testo e decidere che il problema è di difficile risoluzione, è proficuo un approfondimento dello studio teorico delle nozioni inerenti al problema.

9. Bibliografia

[1] A.B.Arons, Guida all’insegnamento della fisica, Bologna, Zanichelli, pp.41-42, 1992;

[2] R.Bagnolesi, Prove scritte di fisica per la Maturità Scientifica Sperimentale: testo e proposte di soluzione, in “Esercitazioni di fisica per la maturità scientifica”, Firenze, Le Monnier,1995;

[3] F.Bassani-L.Foà-F.Pegoraro, Problemi di fisica della Scuola Normale, Bologna, Zanichelli, 1984;

[4] L.Bosman, Il ruolo del “problema” nell’insegnamento della fisica, La Fisica nella Scuola, XVI, 3, p.146, 1983;

[5] L.Bosman, Come si inventa, si prepara e si valuta un test di fisica, La Fisica nella Scuola, X, 3, p.114, 1977;

[6] G.Cavaggioni et Altri, Le Olimpiadi della Fisica. Problemi delle gare italiane e internazionali, Bologna, Zanichelli, 1996;

[7] R.P.Feynmann, La fisica di Feynmann (ed.bilingue), Milano, Masson, 1985;

[8] M.L.Fiandri, Considerazioni sui problemi di fisica, La Fisica nella Scuola, III, 1, p.14, 1970;

[9] T.S.Kuhn, La struttura delle rivoluzioni scientifiche, Torino, Einaudi, p.226, 1978;

[10] D.Gil Perez-J.Martines Torregrosa-F.Senent Perez, L’insuccesso nella risoluzione di problemi di fisica: una ricerca orientata su nuovi presupposti (traduzione di C. Marchi Trevisi),  La Fisica nella Scuola, XXII, nn. 3 e 4, 1989;

[11] D.Halliday-R.Resnick-J.Walker, Fondamenti di fisica. Meccanica, Bologna, Zanichelli, 2001;

[12] C.Marchi Trevisi, I problemi della prof., La Fisica nella Scuola, Quaderno 11, XXXIV, n.2, Aprile-Giugno 2001;

[13] G.Polya, Come risolvere i problemi di matematica. Logica ed euristica nel modo matematico, Milano, Feltrinelli, 1976;

[14] S.Sgrignoli, I problemi di fisica nel concorso a cattedre (1984), La Fisica nella Scuola,  XXIII, 4, 1990, p.131;

[15] C.Wood, Risoluzione di problemi di Fisica (traduzione di C. Marchi Trevisi), La Fisica nella Scuola, XXII, 1989, p.202.

Torna alla pagina precedente