Esempio di risoluzione di un problema di fisica

La seconda fase dell'attività di risoluzione: analisi e discussione del problema.

12 - La risoluzione grafica.

Per chiarire meglio il significato della (1) e le sue conseguenze fisiche, consideriamo adesso il problema dal punto di vista grafico dei diagrammi orari (t,S) dei due moti e tracciamo le due curve sullo stesso sistema di assi cartesiani confrontandone l'andamento.
Ricordiamo che il diagramma orario, o grafico del moto, è un grafico cartesiano che rappresenta il cammino S percorso dal punto materiale sulla traiettoria nei vari istanti di tempo. A seconda del tipo di moto di cui i corpi sono animati esso è rappresentato dalla curva di una funzione algebrica o trigonometrica secondo la rappresentazione simbolica S=f(t), o V=f(t) o, infine, a=f(t).
Nel nostro caso, a seconda dei valori dell'accelerazione (a<0) e della velocità iniziale del rapido (Vo>0), si presentano tre possibili casi, evidenziati dalla Fig. 2. Il primo in fig.2a rappresenta il caso in cui i due treni non si scontrano.

Come si vede chiaramente dall'andamento del grafico di fig.2a, le due curve non si incontrano in nessun punto. Ricordiamo che la retta è il diagramma orario del moto rettilineo uniforme del merci mentre la parabola, con la concavità rivolta verso il basso, rappresenta il diagramma orario del rapido.

Il secondo caso di fig.2b è rappresentato il caso in cui il rapido tamponi il merci in un solo punto.

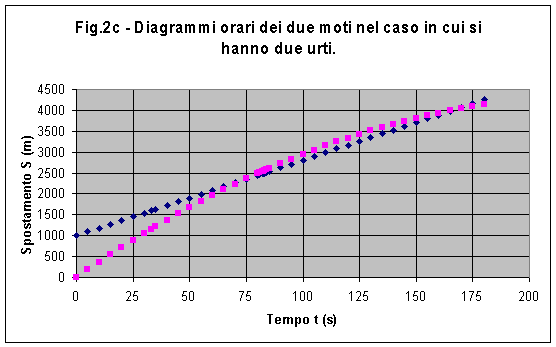
Il terzo caso in fig.2c rappresenta il caso in cui i due treni hanno due urti. Si vede in fig.2c che la parabola interseca la retta in due punti.

Nel caso a) le due curve (la retta con pendenza positiva non passante per l'origine degli assi e la parabola che rivolge la concavità verso il basso, in quanto il moto è ritardato e l'accelerazione è negativa) non hanno nessun punto in comune. Questa situazione si verifica quando risolvendo l'equazione di secondo grado nell'incognita t, il discriminante risulta negativo. In queste condizioni la soluzione dell'equazione non è reale e il problema non ammette possibilità di interazione tra i treni. Dunque, lo scontro non avverrà in quanto in nessun istante di tempo vi è contemporaneità spaziale dei due treni nella stessa posizione, a causa di una soluzione complessa che non possiede significato fisico, poichè un tempo espresso da un numero complesso, del tipo t=(a±ib), non ha fisicamente significato. Peraltro, questo tipo di discussione ha lo scopo di informarci che la condizione proposta non può verificarsi e quindi non può essere accettata e la risposta alla domanda è negativa.
Nel caso b) le due curve hanno un solo punto in comune. Questo caso si ha quando il discriminante dell'equazione è nullo e la soluzione dell'equazione di secondo grado è formata da due numeri reali e coincidenti del tipo t₁=t₂=k. In queste condizioni lo scontro avverrà perchè in un certo istante di tempo ben determinato i due treni occupano la stessa, unica posizione.
Nel caso c) le due curve si intersecano in due punti. Ciò perchè il discriminante è diverso da zero e, quindi, l'equazione ammette come soluzione una coppia di numeri reali e distinti del tipo t₁=k₁ e t₂=k₂. Qui sono previste, dal punto di vista matematico, due posizioni nelle quali i treni si trovano contemporaneamente nello stesso luogo. Fisicamente ciò non ha molto senso, poiché se avviene lo scontro una prima volta è impossibile che si verifichi una seconda volta, anche perchè dopo il primo scontro le condizioni cinematiche rimarrebbero alterate profondamente. E' importante discutere con gli allievi questo fatto. Si deve far capire al giovane che nel mentre il risultato matematico non tiene conto (e non potrebbe fare altrimenti) delle reali condizioni nelle quali il fenomeno evolve, fisicamente è necessario effettuare un intervento di selezione, di scelta, un atto di responsabilità che rende protagonista l'allievo, eliminando quella o quelle soluzioni che escludono la possibilità di manifestarsi concretamente nella realtà. Per esempio è possibile che della coppia di numeri reali che costituisce la soluzione, un tempo t₁ sia positivo e un altro t₂ sia negativo. In questa situazione si deve eliminare il caso t=-k, poiché un tempo negativo rappresenta un intervallo temporale che si riferisce al passato e non al futuro.
In conclusione, da un punto di vista grafico, il problema, per quanto riguarda la prima domanda, è da considerare risolto, perchè la soluzione può essere una sola dei tre casi possibili appena discussi.

Torna all'Indice                                                                                          Pagina successiva