Esempio di risoluzione di un problema di fisica

La seconda fase dell'attività di risoluzione: analisi e discussione del problema.

16 - Seconda e terza domanda.

Passiamo adesso alla seconda domanda. «Dopo quanto tempo i due treni avranno la stessa velocità?».
Qui si chiede di calcolare un intervallo di tempo, cioè il numero di secondi che deve impiegare il rapido onde diminuire la sua velocità fino al valore posseduto dal merci. Appunto quello che è necessario far trascorrere per permettere ai due treni di assumere la stessa velocità. La domanda è perfettamente lecita, in quanto è evidente che il treno rapido in moto rettilineo uniformemente ritardato, diminuendo linearmente nel tempo la sua velocità (cfr. lo schema della Fig.1), dopo un ben determinato intervallo di tempo, che indicheremo con t_U, avrà la stessa velocità del treno merci. Bene. Si chiede quanto sarà questo valore? La risposta è banale perchè essendo la velocità del merci costante l'unico valore in comune non può non essere che la velocità del treno merci. Noi però dobbiamo determinare anche l'intervallo di tempo tU e prima di trovarne la soluzione per via algebrica soffermiamoci attentamente su un altro tipo di diagramma di moto. Quello che vede sia la velocità in funzione del tempo per entrambi i treni, sia l'accelerazione a=a(t). Rappresentiamoli in maniera schematica come segue:

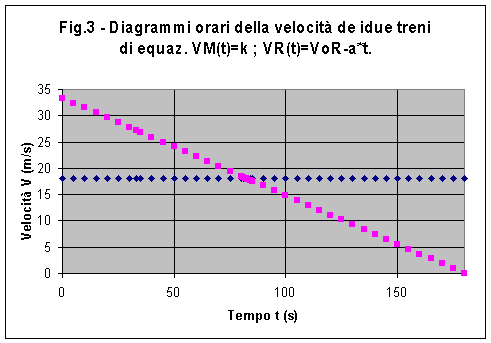
La fig.3, mostra come è l'andamento delle due velocità, quella costante del merci e quella decrescente del rapido.

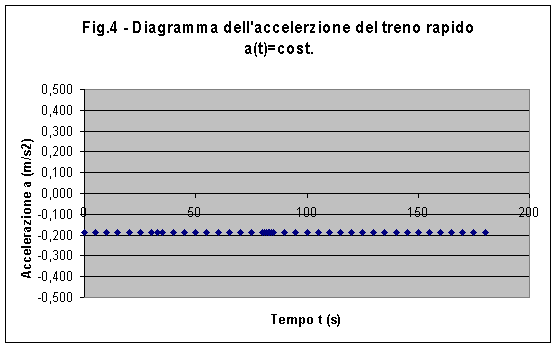
La fig. 4) invece evidenzia la costanza dell'accelerazione del rapido con valore negativo perchè il moto è ritardato. Il treno merci, possedendo una velocità costante, ha accelerazione nulla.

Nella fig. 3), le velocità sono, rispettivamente linearmente decrescente quella del rapido, costante quella del merci. Il punto di intersezione delle due rette possiede il significato di essere, come abbiamo detto in precedenza, l'unico punto che presenta lo stesso valore di velocità per entrambi i treni. Quindi è il valore cercato VU. Ricorrendo al metodo algebrico, possiamo anche qui parlare di condizione di uguaglianza:

V_R=V_M (9)

dove V_R=Vo_R-a t e V_M=cost. Uguagliando i secondi membri si avrà:

Vo_R-a t=V_M

ma, ricordando la (6), a=Vo_R²/2S_F, quindi:

Vo_R-(Vo_R²/2S_F) t=V_M

a condizione che Vo_R>V_M.

Dunque,

t_U=(S_F/Vo_R²) (Vo_R-V_M)=82.5s      (10)

La velocità posseduta da entrambi i treni, nell'istante di tempo t_U, sarà:

V_U=Vo_R-a tU=18.06m/s                 (11)

che non è altro che la velocità del treno merci.

Torna all'Indice                                                                                          Pagina successiva