Esempio di risoluzione di un problema di fisica

La seconda fase dell'attività di risoluzione: analisi e discussione del problema.

20 - Un'ultima domanda.

Ci chiediamo quanto tempo deve trascorrere con il rapido in moto costante Vo_R affinchè si realizzi il tamponamento?
Ragioniamo ancora una volta attentamente. Il problema consiste adesso nel determinare l'intervallo di tempo t_x impiegato dal treno rapido a continuare la sua marcia nonostante il macchinista avesse visto procedere davanti a se il treno merci a velocità notevolmente inferiore alla propria in modo tale da provocare lo scontro in un solo punto della traiettoria.
Dunque, dobbiamo calcolare un intervallo di tempo. Orbene, nella cinematica del moto con velocità costante sfruttando l'equazione oraria del moto rettilineo uniforme del tipo S=V t, dalla quale si ottiene :
 

Dunque, noi possiamo calcolare t (a proposito da questo momento in poi lo chiameremo t_x) qualora conoscessimo S e V. Ma nel nostro caso cosa rappresentano queste due grandezze fisiche? Adeguando i simboli in modo conveniente, otteniamo:
 

dove S_ox rappresenta lo spostamento subito dal rapido tra l'istante iniziale to di avvistamento del merci e l'istante finale tf in cui il macchinista inizia a frenare (evidentemente sarà t_x=tf-to) e Vo_R è la velocità in questo caso costante del rapido.
Come possiamo determinare tx? La risposta è semplice: visto che conosciamo V_oR basta calcolare S_ox. La nostra attenzione si sposta dunque sulla distanza S_ox.
Nella fig.6 è stato ridisegnato il diagramma orario dei due moti.

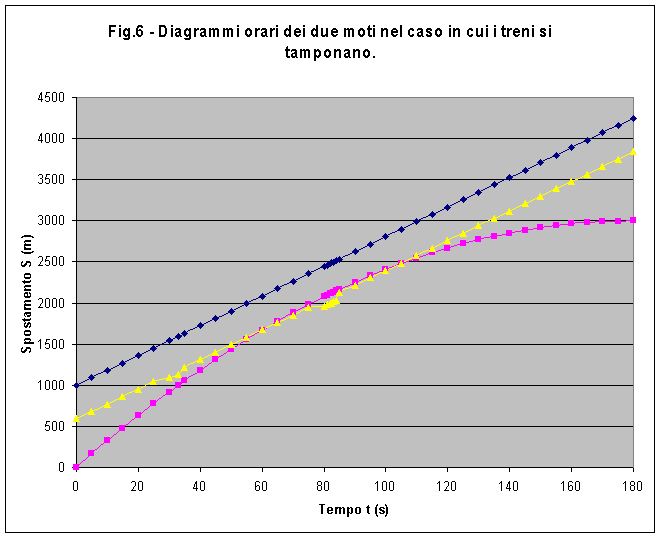
La retta superiore in colore blu rappresenta il moto del merci con S_o, quella intermedia gialla rappresenta il moto del merci con S_ox, mentre la curva in basso arancione il treno rapido.

Riflettendo adeguatamente sul diagramma orario della fig.6 si nota che l'operazione di far scorrere verso il basso la retta S_M=S_o+V_M t equivale a tracciare una retta di equazione S_M=S_ox+V_M t, tangente alla parabola S_R=Vo_R-½ a t² nel punto di contatto P di coordinate (t_U,S_U). Il punto di contatto fra le due curve è determinato da quella situazione cinematica molto specifica, caratterizzata dall'avere come velocità del rapido nel punto P esattamente la velocità del merci, in quanto la tangente alla parabola coincide con la retta che è il diagramma orario del moto rettilineo uniforme del merci.
Dunque, per il moto rettilineo uniformemente ritardato avremo:

V_R=Vo_R-a t

e per il moto rettilineo uniforme sarà:

V_M=costante.

come si rileva d'altronde anche dalla fig.3. E poichè è V_R=V_M, si avrà:

V_M=Vo_R-a t
dalla quale

t=(Vo_R-V_M)/a=82.5 s.

Questo valore di t è tU, come era facilmente prevedibile visto che solo in quel punto entrambi i treni hanno la stessa velocità.
Per determinare, adesso, Sox consideriamo il punto di contatto P. In esso, dal punto di vista cinematico si ha che la distanza S_M del merci dall'origine (S_M=S_ox+V_M t_U) ha lo stesso valore della distanza SR dall'origine del rapido (S_R=Vo_R t_U-½ a t_U²). Combinando e risolvendo rispetto a S_ox si ha:

S_ox=(V_or-V_M)t_U-½ a t_U²=630.21m

La nuova equazione di 2° grado in t_U sarà:

t²-165t+6806.27=0

Il discriminante Δ=b²-4ac=(-165)²-4 1 (6806,27) è proprio uguale a zero a conferma del fatto che le radici dell'equazione di secondo grado in questo caso sono entrambe reali e coincidenti col valore t₁=t₂=t_U=82.5s.
Finalmente, l'intervallo di tempo t_x sarà:

tx=S_ox/Vo_R=18.91 s.

In fig.7 è disegnato il nuovo diagramma orario dei due moti con le varianti apportate dalla nuova situazione fisica che prevede questa volta il tamponamento in un solo punto a causa del fatto che sono cambiate le condizioni iniziali di carattere cinematico che caratterizzano i valori delle grandezze fisiche in esame.

In fig.8 è disegnato il nuovo diagramma orario dei due moti con le varianti apportate dalla nuova situazione fisica che prevede questa volta il tamponamento in un solo punto a causa del fatto che sono cambiate le condizioni iniziali di carattere cinematico che caratterizzano i valori delle grandezze fisiche in esame.

Il diagramma orario del rapido è caratterizzato da due segmenti di retta senza soluzione di continuità che si compongono nel punto in cui il rapido cambia tipologia di movimento.
Il primo segmento (da 0 a 18,91s) è caratterizzato da un tratto rettilineo con pendenza positiva che rappresenta un moto rettilineo uniforme, appunto il moto rettilineo uniforme del rapido alla velocità costante Vo_R durante l'intervallo di tempo tx. Il secondo segmento (da 18,91 a 82,5s) è costituito dal tratto parabolico con concavità verso il basso che si manifesta a causa del moto rettilineo uniformemente ritardato.
Non è previsto il proseguimento del grafico oltre questo istante di tempo perchè, come è facile intuire, lo scontro cambierebbe completamente il fenomeno fisico che perderebbe i connotati di idealità di moto e diventerebbe un fenomeno di urto anelastico.

Vorremmo tirare le somme di quanto detto sopra. Ci scusiamo se ci ripeteremo ma nella risoluzione di un problema la posta educativa in gioco è troppo importante per seguire canoni di estetica di un commento scritto che non prevede ripetizioni.

Le informazioni che possono darci i tre diagrammi orari, cioè a(t), v(t) e s(t) sono profondamente diverse. Infatti, il primo grafico a(t) evidenzia qual'è l'andamento dell'accelerazione del rapido in funzione del tempo. Le informazioni circa la nostra domanda se avverrà o meno lo scontro sono pochissime per non dire nulle. Il diagramma mostra soltanto due rette parallele all'asse delle ascisse. La prima relativa al rapido, nel quarto quadrante (accelerazione negativa), e ci informa che a<0, mentre l'altra retta, relativa al merci, mostra accelerazione nulla, dunque è una retta coincidente con l'asse delle ascisse. Pertanto questo grafico non ci dirà nulla di più che non sappiamo. Anche il secondo diagramma orario non ci aiuta a risolvere il nostro rebus sulla possibilità dello scontro o meno, se e dove avverrà. Osservando la figura si notano due rette, una parallela all'asse delle ascisse è quella relativa al merci e l'altra discendente con velocità decrescente è relativa al rapido. Il fatto che le due rette si intersechino ci dice solo che in quel punto le due velocità del merci e del rapido saranno le medesime. Dopo quell'istante la velocità del rapido sarà sempre inferiore a quella del merci. Nient'altro. L'intersezione delle due rette è avara di considerazioni in entrambi i diagrammi orari discussi finora e non danno risposte sul quesito posto dal problema. E' il terzo diagramma orario che che è una miniera di informazioni e che risponde benissimo alla domanda. Abbiamo già detto che la posizione dei due grafici può rappresentare una delle tre possibilità: che  i due treni non si scontrino, che si scontrino in un punto, oppure che si scontrino in due punti. Il fatto è che i due grafici (fig.6) mostrano che non hanno alcun punto in comune. Dunque non si scontrano. Matematicamente  perchè il discriminante di un'equazione di secondo grado è negativo. Fisicamente perchè non esiste alcun istante di tempo in cui i due treni occupano la stessa posizione. Se si fossero incontrate in un punto, il contatto ci sarebbe stato, anche se istantaneo, con pochi danni. Lo scontro vero sarebbe stato se la parabola e la retta avessero avuto due punti di intersezione. Ma ciò non avviene. Perchè? La ragione riguarda le condizioni iniziali del problema. Certo che se la distanza iniziale fra i due treni fosse stata minore allora lo scontro sarebbe potuto avvenire. Come sarebbe potuto avvenire anche se la distanza fosse rimasta immutata e l'accelerazione, pardon la decelerazione, del treno rapido fosse stata più contenuta. Ma non è stato questo il caso.

Torna all'Indice                                                                                          Pagina successiva