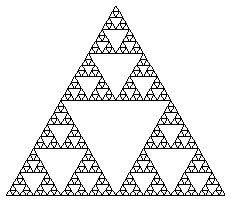La definizione
più semplice e intuitiva descrive un frattale come una figura geometrica
in cui un motivo identico si ripete su scala continuamente ridotta. Questo significa
che ingrandendo la figura si otterranno forme ricorrenti e ad ogni ingrandimento
essa rivelerà nuovi dettagli. Questa proprietà è la cosiddetta
invarianza rispetto al cambiamento di scala, o autosomiglianza. Contrariamente
a qualsiasi altra figura geometrica un frattale invece di perdere dettaglio quando
è ingrandito, si arricchisce di nuovi particolari.

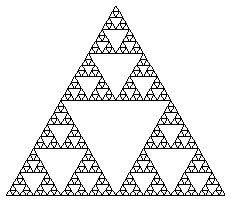
Il
termine frattale fu coniato da Mandelbrot e
ha origine nel termine latino "fractus", poichè la dimensione
di un frattale non è intera. I frattali sono figure geometriche caratterizzate
dal ripetersi sino all'infinito di uno stesso motivo su scala sempre più
ridotta. Questa è la definizione più intuitiva che si possa dare
di figure che in natura si presentano con una frequenza impressionante, ma che
non hanno ancora una definizione matematica precisa: l'atteggiamento corrente
è quello di considerare frattale un insieme F che abbia proprietà
simili alle quattro elencate qui di seguito:
1)
Autosomiglianza: F è unione di un numero di parti che, ingrandite di un
certo fattore, riproducono tutto F; in altri termini F è unione di copie
di se stesso a scale differenti.

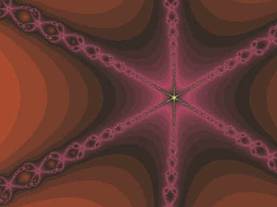
2) Struttura fine: F rivela dettagli ad ogni ingrandimento.




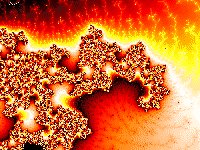

3)
Irregolarità: F non si può descrivere come luogo di punti che soddisfano
semplici condizioni geometriche o analitiche. (la funzione è ricorsiva:
F={Z | Z = f(f(f(...)))}.
4) Dimensioni di autosomiglianza maggiore della dimensione topologica.
I frattali hanno una importante caratteristica: sebbene esse possano essere rappresentate
(se non si pretende di rappresentare infinite iterazioni, cioè trasformazioni
per le quali si conserva il particolare motivo geometrico) in uno spazio convenzionale
a due o tre dimensioni, la loro dimensione non è intera. In effetti la
lunghezza di un frattale piano non può essere misurata definitamene,
ma dipende strettamente dal numero di iterazioni al quale si sottopone la figura
iniziale.
Un esempio di frattale è la curva a "fiocco di neve"
che si può costruire con un procedimento molto semplice. Preso un triangolo
equilatero, si divide ogni lato in tre parti di uguale lunghezza e si costruisce
su ciascuno dei segmenti intermedi che si individuano su ogni lato un nuovo, più
piccolo, triangolo equilatero. La figura che si ottiene somiglia a una stella
a sei punte. Ripetendo il procedimento un numero idealmente infinito di volte,
il risultato dovrebbe essere una figura di area finita, ma con perimetro di lunghezza
infinita, e con un numero infinito di vertici. Nel linguaggio matematico del calcolo
infinitesimale, una curva simile non può essere differenziata. Attualmente
si conoscono e si possono costruire vari tipi di figure con caratteristiche simili,
cioè autosomiglianti, ma è facile comprendere come, nel momento
in cui esse apparvero per la prima volta, nel XIX secolo, sembrarono solo oggetti
curiosi e bizzarri.
Una svolta nello studio sull'argomento si ebbe negli anni
Settanta, con la scoperta della geometria dei frattali da parte del matematico
francese di origine polacca Benoît B. Mandelbrot.
Egli adottò una definizione più astratta di dimensione, rispetto
a quella usata nella geometria euclidea, affermando che per dimensione di un frattale
si dovesse intendere l'esponente della misura delle sue dimensioni fisiche. Il
risultato è che un frattale non può essere considerato come un'entità
avente due, tre, o comunque un numero intero di dimensioni, ma caratterizzata
da una dimensione frazionaria. Ad esempio, la dimensione della curva a "fiocco
di neve" è 1,2618.

La
geometria dei frattali non è semplicemente il frutto di una mera speculazione
teorica, ma trova anche interessanti applicazioni.

Una
costa, se misurata fin nelle sue più piccole irregolarità, tenderebbe
ad avere uno sviluppo infinito, proprio come la curva a "fiocco di neve".
Mandelbrot suggerì che le montagne, le nuvole, i raggruppamenti di galassie
e altri fenomeni naturali potessero essere considerati esempi di frattali naturali;
da ciò, l'applicazione della geometria dei frattali alle scienze vide un
rapidissimo sviluppo. Inoltre, la bellezza dei frattali li ha resi un elemento-chiave
nel campo della grafica per computer.
Nel 1987, il matematico di origine britannica
Michael F. Barnsley scoprì la trasformata frattale, che rivela automaticamente
i codici frattali nelle fotografie digitalizzate. La scoperta inaugurò
la tecnica di compressione delle immagini in diverse applicazioni multimediali.

Torna
all'inizio della pagina